Раздел: Документация
0 ... 56 57 58 59 60 61 62 ... 96 Принцип получения формул поясняется графиком: + о igvmin 0 lgVmax и последовательностью действий. 1. Перенос начала координат в точку (У: х\ = lgV -(У, посередине между min и max; c = igvn lg max lg min AVAV = lgmax ~ - =>x\ =lgV"lgVmax + -. 2. Сжатие шкалы, т.е. преобразование подобия, Х\ = Кхх, причем К находим из условия Х\ = 1 при lg V = lg Vmax. 2lgV-lgVmax +1 g rnax lg min Перейдем от переменных V, 5, Z к переменным , #2, #3. lg A# = у = lg Po + Pi lg V + p2 lg S + P3 lg Z. Выразим переменные lg V, lg 5, lg Z через , x2, X3: Ogmax -Igmin)*! = 21g V - 21g Vmax +lgVmax - lg Vmm ; т/ lg max "Igmin v , lg max +g min . lgV----xx +---, e/=lgp0 +Pt lgVmax ~]gV™" xx +ft lgVmax +18ymin + +o Igmax -Igmin +o Igmax + lgmin 2222 +p2 max ~lmin x + Igmax +lgmin. У=ЬохО-Ь\х\ +b2x2 +b3x3] X0 =1 feo=igp0+Pilgymax;lgymin + l§ тах 1§ 8тах 1б тах 8 п ь2 = Р2 Ьз =Рз 8 тах 8 zt\ Мы установили однозначное соответствие между переменными У, 5, Z и *t, х2, *3, и между параметрами р0, Pi, р2, Рз и Ь0 Л > Ь2 > Ь3 • В пространстве переменных х\, д, *з параллелепипед переходит в куб с центром в начале координат и ребром, равным двум. 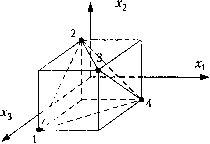 Фигура, образованная точками 1,2,3,4 называется симплексом. В данном случае имеем правильный симплекс. Если эксперимент ставить в вершинах куба, то мы имеем так называемый полный факторный эксперимент (ПФЭ) типа 2п, где п -число факторов. ПФЭ реализует все возможные комбинации уровней независимых переменных, каждая из которых варьируется на двух уровнях. Матрица координат вершин куба называется матрицей плана эксперимента. При линейном росте числа факторов число опытов растет по показательной функции. Если при решении задачи моделирования можно ограничиться линейным приближением, то ПФЭ неэффективен. Применяется дробный факторный эксперимент. Половина факторного эксперимента называется полурепликой и т.д. Для нахождения оценок В последовательно находим матрицы: Xt ХХ, (ХХ)"1, (ХХУХ, (XX)XY =£. Статистический анализ уравнений регрессии. Результаты наблюдений или измерений величины У ={у\ ,у2,..,Ум} являются случайными величинами. Действительно, если мы настроим станок на один и тот же размер статической настройки Aq и на одном и том же режиме будем обрабатывать детали, то измеренные размеры деталей будут разными. На точечной диаграмме показаны зависимость размера от ее номера. 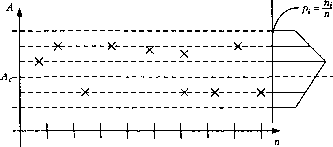 попадания в размерный интервал Полем рассеяния называется разность со = Лтах - Атт . Разделив со на К - число интервалов, можно подсчитать количество деталей, попавших в г-й интервал и статистическую вероятность, или частность pi =-. п В реальных задачах п всегда ограничено и называется объемом выборки. Совокупность п измерений называется выборкой из некоторой генеральной совокупности. Таким образом, наблюдая или измеряя некоторую случайную величину Х} мы можем говорить о последовательности наблюдаемых значений Х\, х2, • . • , хп , как о совокупности значений одинаково распределенных независимых случайных величин Х\, Х2, . • . , Хп , представляющих п экземпляров одной и той же случайной величины X. Поэтому все выборочные характеристики - суть функции случайной величины, т.е. они сами случайны. Например: Хл + Х-)+...+Хп х - ----- - статистическое среднее п - Хл + Х2+...+Хп 7 или X =------, т.е. х = А - случайная величина. М[х] = тх , D[3t ] = ОД ] + -L ]+• •.+ Л WXn ] = п2пгп1« 0 ... 56 57 58 59 60 61 62 ... 96 |












