Раздел: Документация

0 ... 57 58 59 60 61 62 63 ... 96

Статистическая дисперсия S2 = - У(д - х)2

п

Если случайная величина X зависит от других случайных или неслучайных величин, например У = ifix ,Х2,х3) или Ад = fiV,S}Z)} то зависимость М[У] = f(x\ ,х2 ,х%) называется регрессией случайной величины У по величинам Х\, Х2, Х3.

Поэтому мы говорим о регрессионных уравнениях или регрессионных связях. Регрессионные уравнения подвергают статистическому анализу.

Классический статистический анализ состоит из следующих шагов.

1.Делается предположение (выдвигается гипотеза, что наблюдаемая величина У распределена по нормальному закону).

2.Проверяется гипотеза о нормальности при помощи так называемых критериев согласия. Наиболее часто употребляемые - критерий Пирсона или Колмогорова.

Суть критериев в следующем: сравнивается теоретическое и статическое распределение:

п2

TCJ f(x) - - I = Krj - критерий Пирсона.

Ы \ п)

р(Кп < К rj ) = ос, где а - доверительная вероятность, К п - пороговое значения критерия, по а находят Кп и сравнивают с Кп.

Если неравенство выполняется, то говорят, что с вероятностью а (например, 95%) величина X распределена по нормальному закону.

max

fix)-

= Кк - критерий Колмогорова.

3.В каждой точке факторного пространства делают т параллельных опыта, т.е. реализуется т матриц плана эксперимента.

4.Результаты опытов в каждой точке усредняются.

- 1 -ит Т1

Y9 =-2>1я,

где Уд/-й эксперимент в g-и точке факторного пространства.

I m

5. Вычисляют дисперсию Sg = - У/У -Уд)2.

6. Проверяют однородность (одинаковость) дисперсий в точках факторного пространства при помощи критерия Кохрена.

---

G =

д max

<G,

кр

= а.

По а находят Gp и проверяют выполнение неравенства.

7.Рассчитывают коэффициенты В по формуле: В =(х х)~х ху.

8.Проверяют значимость каждого коэффициента, т.е. выдвигают гипотезу: Ьг>0. Это делается при помощи t - критерия Стъюдента.

p\ti =

M->t

= а.

Распределение Стъюдента t. а => tKp.

9. Проверка адекватности модели исследуемому явлению при помощи критерия Фишера. (\

F =

уад

кр

= а;

ад

<7=1

2.2.8. Непрерывные оптнмизационые задачи

Назначение оптимального режима обработки, для технологической системы (рис.2.32).

ТС - токарная обработка. Целевая функция - себестоимость.

л G0 п nde ( Ev

0 = --, где Сп =- Ес +

VSи 10001 с Т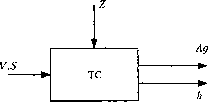

Рис.2.32. Технологическая система как объект управления

---

<7 = p20yp2,5p23Zp23 j

уравнения объекта управления.

В партии деталей Z меняется от Zmin < Z < Zmax. Отсюда

47max -Agmin = VS (ZPX - zj" ) = 0,7 = Tg,

если > 0

tT

h = jqdt\ hT = jqdt <АД0П => VSZT доп>

где q - скорость износа инструмента. Запись оптимальной задачи.

e=-->min; VS v,s

V < V < V

v min - v - v max >

° min - ° - Jmax »

р20УР215Р23 221Г<

*ДОП •

Логарифмированием можно свести задачу к линейной, относительно логарифмов переменных. (Логарифмирование не сдвигает экстремальные точки функции, например,

Y = /•(*); ф(У) = ф(/хх));

,е/ф е/ф df с/ф v

если ф - монотонная функция, то и -1 = -1 -- и -1 > 0J

rfx f dx df

lg6=lgCe -lgV-lgS; lgVmin <lgV<lgVmax;

0 ... 57 58 59 60 61 62 63 ... 96