Раздел: Документация

0 ... 55 56 57 58 59 60 61 ... 96

Произведение матриц некоммутативно. Скалярное произведение векторов коммутативно:

ах\\ = а2Ь2 =г\а\ +Ь2а2.

Транспонирование - замена строк столбцами, и наоборот. А и А. Свойство (АВУ = В А. Доказательство:

AxB=C,Cik =Ak Bk , стр. столб.

Cik=Cki=Ak В{ = В{ Ak =В{ Ak .

стр. столб. столб. стр. стр. столб. . Свойство обратной матрицы. Обратная матрица АА"1 = А-1 А - 1 - единичная матрица.

Скалярное произведение *2

ЕЕ =(ее2...eN) х

2 22

= et + e+...+ef. 12N

-скалярный квадрат вектора. Выражение для скалярного квадрата будет

У = ХВ + Е => Е = У - ХВ; Е = У - ВХ;

ЕЕ = (У - BX)(Y - ХВ) = YY - BXY - YXB + ВХХВ =

= YY -2BXY + BXXN = SR

-остаточная сумма квадратов.

Здесь мы использовали свойство В X У = У ХВ, так как Таким образом, SR = /"(В). Чтобы найти min, надо

Mr дВ

= 0 =

Sb0

Sb,

dSR KSbn J

= 0.

To есть нам надо продифференцировать выражение для SR.

---

Вспомним элементы векторного дифференцирования.

dYY dlBXY

дВ

В1 А= (Ь0Ь,) х дВХХВ

дВ

= 2XY; XY = A=\ дВА

а2

; s = (Vi);

as

Ka2j = 2ХХВ.

= Ь0ах +Ь\а2;

дВ

К.а2

X X - симметрическая матрица, так как (X X) = X X;

XY = A =

(b0 bj) х

aUа2\

а2\а22

Unапл

а2\а22

; Причем а\2 - #21 В ~ = (b0 fy)x

аиЬ0 + ank ) a2\h + 221

= аиЬ2 +апЪф\ +а2фоь\ + *22bt2

- квадратичная форма вектора В. Дифференцируем по Ь$ и fy .

а2\ь0 + 221,

as*

*11 й12 *12 *22>/

Ч6! v

Отсюда

= 2А£.

= -2Х Y + 2Х ХВ =>ХХВ= X У;

(X X)"1 (X Х)В = (X X)"1 X YB = (X X)"1 X У.

Проведенные преобразования носят название метода наименьших квадратов - М.Н.К.

Свойства оценок, полученных М.Н.К.

1.В - являются линейными оценками.

2.В - являются несмещенными оценками. Доказательство: М[У] = ХР;

М[В] = М[(Х X)"1 X У] = (X X)"1 X М[У] = = (X X)"1 X Хр = р; М[£] = 0.

3.В классе линейных несмещенных оценок оценки, полученные методом М.Н.К., обладают минимальной дисперсией (теорема Гаусса-Маркова).

---

Планирование экспериментов. М.Н.К. минимизирует дисперсию на множестве методов вычисления оценок. Дисперсия также зависит от расположения точек в факторном пространстве. Минимум дисперсии доставляет ортогональный план, задаваемый ортогональной матрицей (теорема Бокса).

Рассмотрим на примере получение ортогонального плана и расчет коэффициентов В.

Конкретизируем вид зависимости Ад = f(V,S,Z).

Выдвинем гипотезу, что Ад =Ро

Степенная зависимость выдвинута из следующих соображений для степенной функции у =сха при различных а получаем следующие различные графики: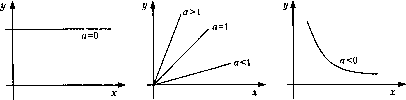

Переменные меняются в некоторой области, задаваемой неравенствами:

V < V < V v min - v - v max

° min - ° - ° max

7 < 7 < 7 min - - max

параллелепипед в пространстве факторов У, 5, Z.

Логарифмированием выражение для Ад приводится к линейному относительно логарифмов.

Введем обозначения:

21gV-lgymax

11 tt"1тг

Х2 =.---- - + j;

#3 =---~ - + 1.

lmax "lemin

2\gV-	IS max
IS max	8 min
21g5-	1§ max
Smax	-ISmin
2\gZ-	* ISmax

0 ... 55 56 57 58 59 60 61 ... 96