Раздел: Документация
0 ... 54 55 56 57 58 59 60 ... 96 Рис.2.30. Технологическая система -вых x".7w - выходное положение элемента формы заготовки, относи- тельно технологической базы, переменные ТП. У ji ~ управляющие переменные ТП. 9,г - критерий оптимальности. пример: токарная обработка (рис.2.31). Обрабатываемая деталь 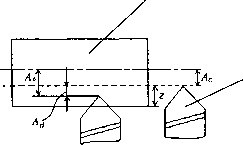 Инструмент (резец) Рис.2.31. Схема токарной обработки Здесь: Лс - размер статической настройки, Лд - размер динамической настройки, Ад - технологический размер, Лд = Ас + Лд. В рассматриваемом примере переменные, описывающие ТП, следующие: *вых =(ЛД)Ла,/гзад); хш =(z,H);Y = (V,S), где Ra - шероховатость поверхности детали, Нзад - износ инструмента, z - припуск на обработку, Н - твердость материала заготовки, V -скорость резания, S - подача. Отдельного рассмотрения заслуживает критерий 9. Одним из возможных критериев является себестоимость работы ТС по преобразованию заготовки в готовую деталь. Она слагается из двух частей: Q=EctM + Еи где Ес - стоимость станкоминуты, Еу[ - стоимость работы инструмента за Г, £м ~ машинное время, Т - период стойкости инструмента. t11 = ndl М S0-n SM 1000vs ЮООУ ft ndl ndl C0 rp. n =- 0 =-Er + Елл-= -- при T = const; nd1000vs c и 1000vst VS C0 = ndl 1000 с г где Sq - подача на оборот детали, ~ минутная подача. Таким образом, можно описать ТС следующими зависимостями: хвых =/7(хвх7) или Лд =/;(у,5)2,Я), =/*2(,5,2,Я), зад =f3(V,S,Z,H\ 6 = Ф(д:БХ,7)или 6=ф(У,5). Подобные модели в отличие от графовых называются непрерывными, или параметрическими. Задачи статистического моделирования (применительно к моделям ТС). Под моделированием или выяснением механизма явлений мы будем понимать следующую задачу. Имеется некоторый объект А, обладающий входом х и выходом у. Объект А переводит множество входных величин X в множество выходных Y. Элементы множеств X и Y могут быть скалярами, векторами, функциями. Требуется определить структуру объекта А на всем множестве X, или вид преобразования. Возможно два различных подхода: аналитический и статический. ТП - есть пример сложной диффузной системы. Будем рассматривать вход - вектор, выход - скаляр, т.е. у =/X*i ,*2> При этом математическое описание - отрезок ряда Тейлора. ппп У=Ь0 + ZjbiXi + HhiJXiXJ + 2b»*,2+"> i=l»<1t=l где ь0 = */о; = -Ч = ; ь« =-у Вводя новые переменные типа: хп + \ =Х\Х2\ хп + 2 ~х\хз> хп + г -х2 и т.п., приходим к искусственной линейной форме вида: y=bQXQ+ b2x2+...+bkxk, где si. Задача: определить коэффициенты 6q, b\, . . . bk по результатам эксперимента. Сгц*12...*1*) -> У1; У1 = fy)*0 + bi*ll+--+bfc*i* + в1 (x2XX22...X2k)-±y2\y2 = Ь0*0 + Ь1*21+--+ЬЛ + е2 (xmxN2...xNk) -yN\ yN = b0x0 +btxm+...+bkxNk + eN. Вводим матричные обозначения:
X - матрица плана эксперимента, хц - точки факторного пространства (точки пространства эксперимента). Тогда У = ХВ + £. Вспомним матричные операции. Произведение Ах В = С => Cik = AjBk - скалярное произведение строки на столбец. Количество столбцов матрицы А равно количеству строк матрицы В. dinvl =рх dimB = qx s, dimC = p x s. В скалярной форме 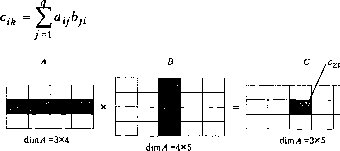 0 ... 54 55 56 57 58 59 60 ... 96 |












