Раздел: Документация
0 ... 58 59 60 61 62 63 64 ... 96 \gSmin <lgS<lgSmax; Pit lgV + p12lg5<lg тд P21 lg+P22 lgS<lg h доп Ргор23 Уравнение граничной линии - Рц lg V + fy2 lg = a. Отсюда lg 5 = -- lg У + -. Pi 2Pl2 Из физического смысла задачи знаки коэффициентов рц <0, Pl2 >о> Р21 >0> Р22 >0- Рассмотрим геометрическую интерпретацию задачи линейного программирования. Заметим, что grad lg 0 = I -1J Voiit Чпах. gy 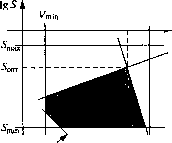 grad G Мы рассмотрели простейший случай однопереходной обработки. В случае многопереходной обработки, количество переменных увеличивается, и между ними возникают связи. Это показывает следующий пример (рис.2.33). Каждую ТС будем рассматривать как ориентированный объект (см. рис.2.30). Имеем 6 ТС: / = 1.3; ij = 12. ТС ji совпадает с припуском Zjj. Запишем выходы и входы всех технологических систем: ВЫХ о „ВЫХ /• „вых г„вых о„вых л „вых 7 *11 = 3> х\2 =Ь, х2\ =5,Л22 =0,31 =4, *32 =7, 4? = 2, *182Х =4, д:2вГ =1 + 3-2, *£2Х = 5 + 6 - 4, х% = 3, *2Х = 6, / =7, II =8. 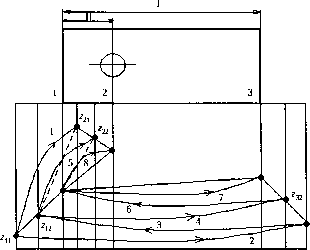 Рис.2.33. Пример связей при многопереходной обработке Изобразим совокупность ТС виде многомерной системы регулирования (рис.2.34). В нее как бы входят размеры заготовки, выходят размеры детали. Уравнения системы: ХТ =/iiWiXii> = /ii(2ii)=3Bi =3> ХТ = /31 <*" .У31 > = /31 (/ii ЦТ .Уи )У31 > = <2Х = * ТС,, %1 тс31 тс„ 132 7=1 -► 1-2 тс2- 8=11 Рис.2.34. Связанная совокупность ТС v12 гвых 132 /322>32) = -ВЫХ .вых с22 : /з2 (/i 2 (/з! (fi 1ЦТ > У\ 1 )3i 2 )32) = 7 = /; = /"21 .У21 > = /21 (0~2 + /ii C2,Fi 1 »У21) = 5; В/32<*ИУ22) = V21 «1 - 2 + /5, (2,Fi 1 »F2i» - = /"22 -(/31 Vii ЦТ .Fll >У31» + ч-К/12</з1 Vll ЦТ »Fll )У31 )Fl2».F22 Запись оптимальной задачи, ю, < Г,, (О) j Г) j - ограничения = 8 = 7/. min - целевая функция. Решение оптимизационных задач рассматриваемого вида, т.е. оптимизация при наличии ограничений - неравенств, называется задачей математического программирования. Решению задач математического программирования посвящена многочисленная литература. 0 ... 58 59 60 61 62 63 64 ... 96 |












