Раздел: Документация
0 ... 105 106 107 108 109 110 111 ... 143 Рис. 10.17. Представление нелинейной САУ в ви- , де последовательного соединения нелинейного эле- К0Кд[%) ft/ju) мента НЭ и линейной части ЛЧ системы.>{"flj~ £лЧ = koNn (со) eV*; Z0 (А/а) = N0 (А/а) еГ*л*п, получим k0Nn (со) е* = N0 (А/а) е/ЫА/а>.(10.21) Из последней формулы видно, что в системе возможны колебания, если одновременно удовлетворяются два условия: &0гУл (со) = N0 (А/а), фл (со) = % (А/а)(10.22) или в логарифмическом масштабе 20 lg k0N„ (со) = 20 lg N0 (А/а)(10.23) и iM<o) = *.№)-(10-24> Первое условие будет выполняться при пересечении логарифмических амплитудных характеристик линейной части и нелинейного элемента, а второе условие — при пересечении их фазовых характеристик. Колебания в системе будут возможны, если точка пересечения амплитудных характеристик и точка пересечения фазовых характеристик соответствуют одной и той же частоте. Методика построения логарифмических частотных характеристик линейной части системы не требует пояснений. Для построения логарифмических частотных характеристик нелинейного элемента найдем выражения для ее амплитудной и фазовой характеристик. Имея в виду, что Na (А/а) = I--. * . I = — 1, получаем следующее выражение для логарифмической амплитудной характеристики нелинейного элемента: L0(А/а) = 20lgN0(А/а) = — 20 lgYq20(A/a) + b20(A/a). (10.25) Выражение для фазовой характеристики нелинейного элемента ф0 (А/а) = arg (— 1/К0 (А/а)) = arg (1/К0 (А/а)) - 180°, следовательно, *.(4Hrd« (-i££r)-180°-(10.26, В случае безынерционных нелинейных элементов, как следует из формул (10.25) и (10.26), амплитудные и фазовые характеристики не зависят от частоты и представляют собой прямые, параллельные оси абсцисс. На рис. 10.18. изображены ЛАЧХ L„ (со) = 20 lg k0N„((a) и фа-зо-частотная характеристика 1]}л (со) линейной части системы, а также 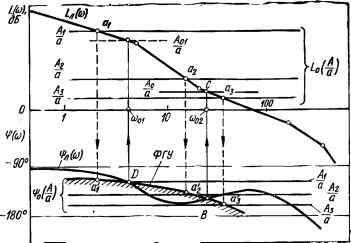 -£7- Рнс. 10.18. Исследование автоколебаний нелинейной системы методом ЛЧХ. нанесено семейство амплитудных L0 (Ala) = 2(W0 (А/а) и фазовых % (А/а) характеристик нелинейного элемента при различных значениях А/а. Для исследования возможности автоколебаний, определения их устойчивости и параметров удобно пользоваться фазовой границей устойчивости (ФГУ) колебаний [59]. Для построения ФГУ, в соответствии с условием (10.23), отмечаются точки пересечения амплитудных характеристик линейной части и нелинейного элемента (точки at, а2,...) и сносятся по вертикали на соответствующие фазовые характеристики нелинейного элемента в точки а\, а2, ... Кривая, проведенная через эти точки, и является фазовой границей устойчивости колебаний. Если фазовая характеристика линейной части пересекает кривую ФГУ (см., например, точку В, рис. 10.18), то это значит, что амплитудные характеристики и фазовые характеристики линейной части и нелинейного элемента пересекаются в точках (С и В), соответствующих одной и той же частоте со02. Следовательно, при этом одновременно удовлетворяются условия возникновения колебаний (10.23) и (10.24). Частота автоколебаний со определяется непосредственно по шкале частот, а относительная амплитуда А0/а — интерполяцией между значениями А/а на ближайших характеристиках нелинейного элемента, расположенных выше и ниже точки пересечения С. Согласно рис. 10.18 в нелинейной системе возможно возникновение автоколебаний с частотами и относительными амплитудами соответственно со01, А01/а и со02, AJa. Условие устойчивости автоколебаний рассмотрим на примере автоколебаний со02 и AJa (точки пересечения характеристик В, С). Оно состоит в следующем. При увеличении амплитуды автоколебаний до A la — А0/а + АА/а (пересечение амплитудных характеристик пере мещается из точки С в точку а3) система должна стать устойчивой, чтобы амплитуда автоколебаний уменьшилась до прежнего значения A J а. Это требование будет выполняться, если на частоте ©ог, соответствующей точке а3 пересечения амплитудных характеристик, фазовая характеристика линейной части \рл (со) идет выше кривой ФГУ, как показано на рис. 10.18. При уменьшении же относительной амплитуды до AJa = AJa — АА/а (пересечение амплитудных характеристик перемещается из точки С в точку а2) система должна стать неустойчивой, чтобы амплитуда автоколебаний увеличилась до AJa. Данное требование будет выполняться, если на частоте со02, соответствующей точке а2 пересечения амплитудных характеристик, фазовая характеристика я)эл (со) проходит ниже кривой ФГУ, как показано на рис. 10.18. Таким образом, согласно приведенному условию автоколебания с параметрами со02 и AJa будут устойчивы, а с параметрами «и А01/а — неустойчивы. Применительно к САУ, у которых ЛАЧХ лиг: яой части не имеет участников с положительным наклоном, это общее правило дает простой способ исследования устойчивости автоколебаний. Если при увеличении А/а амплитудная характеристика нелинейного элемента перемещается вниз, то кривая ФГУ штрихуется снизу (как показано на рис. 10.18), если же она перемещается вверх, то — сверху. Автоколебания будут устойчивыми, если фазовая характеристика линейной части системы при увеличении со пересекает фазовую границу устойчивости, переходя с заштрихованной стороны на незаштрихованную. На рис. 10.18 точка В пересечения фазовой характеристики линейной части системы с кривой ФГУ при со02 соответствует устойчивым автоколебаниям с относительной амплитудой AJa, а точка пересечения D соответствует неустойчивым колебаниям на частоте со01 с относительной амплитудой А01/а. В случае применения безынерционных нелинейных элементов с однозначной нелинейностью исследование автоколебаний системы несколько упрощается. В этом случае коэффициент гармонической линеаризации Ь0 (А/а) = 0, поэтому в соответствии с формулами (10.25) и (10.26) т. е. амплитудные характеристики будут представлять собой семейство параллельных оси абсцисс прямых, соответствующих различным значениям А/а, а фазовая характеристика, а следовательно, ФГУ для всех однозначных нелинейностей совпадают с линией гз (со) = —180°. В качестве примера исследуем устойчивость и автоколебания системы с релейным элементом, имеющим однозначную характеристику с зоной нечувствительности (см. табл. 10.1). Пусть ЛАЧХ Ln (со) = = 20 lg koN„ (со) и фазо-частотная характеристика г)л (со) линейной системы имеют вид, изображенный на рис. 10.19. L0(A/a) = — 20 \ga0(A/a), q0(A/a) = — 180°, (10.27) (10.28) 0 ... 105 106 107 108 109 110 111 ... 143 |












