Раздел: Документация
0 ... 102 103 104 105 106 107 108 ... 143 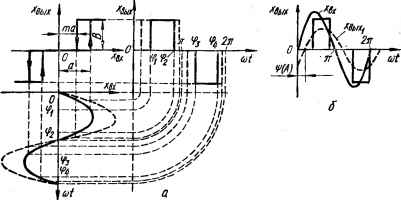 Рис. 10.11. эквивалентном коэффициенте элемента. понятию об комплексном нелинейного характеристикой, изображенной на рис. 10.11, а. Если на вход этого нелинейного элемента подавать гармоническое колебание х = = A sin at, то на его выходе получим периодическую функцию хвых (/) в виде прямоугольных импульсов (рис. 10.11, а), т. е. функцию, отличную от синусоидальной. Выходная величина нелинейного элемента, обладающего любой другой статической характеристикой, также будет представлять собой соответствующую периодическую функцию, отличную от синусоидальной, т. е. нелинейный элемент вносит искажения сигнала. Суть метода гармонической линеаризации состоит в том, что выходная периодическая функция нелинейного элемента разлагается в ряд Фурье, т. е. представляется в виде бесконечной суммы гармонических колебаний. Если линейная часть системы является фильтром, ослабляющим высшие гармоники до пренебрежимо малых значений, т. е. выполняется гипотеза фильтра, то из рассмотрения отбрасываются все гармоники высшего порядка и считают, что выходная величина нелинейного элемента представляет собой первую гармонику разложения (рис. 10.11, б): *вых = f (*вх) = f (A sin со/) ~ л;ВЫХ1 = q (A) sin to/ -f V (A) cos со/, (10.8) где q (А) и b (A) — коэффициенты первой гармоники ряда Фурье: 2Я q (А) = --\ f(A sm ш0 su1 (utdtot; о 2Я ИЛИ сУ (А) = — f f (Л sin со/) cos со/dco/, -Wi = Л (Л) sin [со/ + ф (Л)], (10.9) где Ах (Л) = Vq (Л) + ЬЛ (Л) — амплитуда первой гармоники; Ф (Л) = arctg lb (A)/qf (Л)] — сдвиг по фазе первой гармоники относительно входного колебания. Запишем комплексные изображения входной и выходной (первой гармоники) величин нелинейного элемента: ■вх = А&1 \ хвых, = <f (А) е°* + V (А) /е/ш = А, (А) е. Отношение комплексных изображений первой гармоники выходной величины и входного колебания называется эквивалентным комплексным коэффициентом усиления нелинейного элемента (гармонической передаточной функцией) К9АА)===q(A) + jb(A), (10.10) где q (А) = q (А)/А, Ь (А) = Ь (Л)/Л — коэффициенты гармонической линеаризации. Эквивалентный комплексный коэффициент усиления (ЭККУ) можно представить в показательной форме К,н (А) - N (Л) е = ЛМ)ГФИ)] = е/ФМ). (Ю-11) где N(A) = Vq*(A) + b2(A) = Лх (Л)/Л — модуль ЭККУ; гз(Л) = = агст£[6(Л)/<7(Л)] = ср(Л) — аргумент ЭККУ, т. е. модуль N(A) ЭККУ показывает, во сколько раз амплитуда At (А) первой гармоники выходного колебания отличается от амплитуды А входного колебания, а аргумент ф (А) ЭККУ равен разности фаз между этими колебаниями. С учетом (10.11) комплексное изображение первой гармоники выходной величины нелинейного элемента хвмх1 =/С,„(Л)хвх = N{A)e™A> ■ Леш = А1{А)е*0,™йа, где Лг (Л) = N (А) А. Из выражений для N (Л) и ф (Л) видно, что модуль и аргумент эквивалентного комплексного коэффициента усиления нелинейного элемента Кэ.н (А) зависят от амплитуды Л входного колебания и не зависят от частоты. Зависимость модуля N (Л) ЭККУ от амплитуды входного колебания можно объяснить зависимостью длительности выходных импульсов нелинейного элемента от амплитуды входного колебания (рис. 10.11, а): с увеличением Л длительность импульсов увеличивается, а следовательно, увеличиваются амплитуда первой гармоники выходного колебания и модуль N (Л). Зависимость же аргумента чр (j4) ЭККУ от Л объясняется зависимостью расположения середины выходных импульсов нелинейного элемента относительно фиксированных точек л./2, Зл/2, ... на оси at. С увеличением Л импульсы перемещаются на оси at влево и сдвиг по фазе (запаздывание) яр (Л) первой гармоники Хвых1 выходного колебания относительно входного колебания уменьшается. Возможный вид зависимости модуля и аргумента ЭККУ нелинейного элемента от амплитуды входного колебания представлен на рис. 10.12. ЭККУ нелинейного элемента К9.а (Л) геометрически изображается вектором, модуль которого равен N (Л), а аргументу (Л). С изменением N(A) 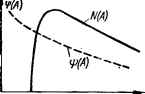 Рис. 10.12. Возможный вид зависимостей модуля N (л) н аргумента ф (А) ЭККУ от амплиту-ды входного колебания. 0 А амплитуды Л входного колебания N (А) и я) (А) изменяются. При этом конец вектора Кэ.и (Л) описывает кривую. Годограф вектора Кэ.и (А) при изменении амплитуды входного колебания называется эквивалентной амплитудно-фазовой характеристикой нелинейного элемента. Таким образом, гармоническая линеаризация состоит в замене нелинейного элемента, описывающего уравнением хвык = f (хвх), эквивалентным линейным, который осуществляет такое же преобразование гармонического входного сигнала, как и нелинейный элемент; уравнение эквивалентного элемента линейно: Функция Кэ.в (Л) эквивалентного линейного элемента является аналогом функции К (/ш) линейного элемента. Отличие между ними состоит в том, что первая зависит от амплитуды Л входного колебания, а вторая — от частоты со этого колебания. В том случае, когда выходной сигнал хВЬ1Х нелинейного элемента зависит не только от входного Хвх, но и его производной dxBJdt, т. е. Хвых = / (-Квх, dxex/dt), эквивалентный комплексный коэффициент усиления является функцией как амплитуды Л, так и частоты со входного сигнала: Методика определения эквивалентного комплексного коэффициента усиления нелинейных элементов Рассмотрим сперва методику определения /Сэ.н (Л) нелинейного элемента с однозначной статической характеристикой на примере релейного элемента (рис. 10.13, а). Для этого на его вход подадим синусоидальное колебание (рис. 10.13, б). На выходе элемента получим последовательность прямоугольных импульсов (рис. 10.13, е). В соответствии с формулой (10.10) Из рис. 10.13, е, г видно, что на участке от 0 до со х = ■= f (Asincot) = 0. Следовательно, при определении q (Л) интегриро- Кэж (Л, /со) = q (Л, со) + \Ъ (Л, со) = N (А, со) е K*u{A) = q(A) + jb(A). Согласно выражениям (10.9) и (10.10), 2я q (Л) =. -£JL = -ij- j / (Л sin cor) sin ride*. 0 0 ... 102 103 104 105 106 107 108 ... 143 |












