Раздел: Документация
0 ... 100 101 102 103 104 105 106 ... 143 ками. Решения, соответствующие этим участкам, сшиваются. Метод отличается сложностью вычислений, особенно, если порядок уравнения системы высок. Графоаналитические методы. Среди них наиболее распространенным является метод построения переходных процессов Д. А. Башки- • рова. Он основан на разложении сложного дифференциального уравнения на элементарные уравнения, для которых предложен простой графический способ интегрирования. Метод пригоден для линейных и нелинейных систем практически любого порядка. Численные методы. Сводятся к численному решению нелинейных дифференциальных уравнений. В последнее время широко применяются в связи с использованием цифровых вычислительных машин для исследования систем автоматического управления. Метод малого параметра. Применим для анализа псевдолинейных (почти линейных) систем, в нелинейные дифференциальные уравнения которых входит некоторый (малый) параметр р. так, что при нулевом значении р нелинейные уравнения вырождаются в линейные. Метод статистической линеаризации, дающий возможность оце- . нить точность нелинейной системы при случайных воздействиях. Сущность метода статистической линеаризации состоит в том, что нелинейный элемент заменяется эквивалентным линейным элементом, который одинаково с нелинейным, преобразует два первых статистических момента случайной функции: математическое ожидание (среднее значение) • и дисперсию (или среднее квадратическое отклонение). Метод одновременно предложен И. Е. Казаковым (СССР) и Р. Бутоном (США). Моделирование на электронных моделирующих установках, позволяющее повысить точность и скорость исследования нелинейных систем. > Моделирование оказывается наиболее эффективным методом исследо- ■>.■ вания систем, когда из-за их сложности другие методы становятся ма- -лоприемлемыми. Метод пространства состояний. Удобен для исследования нели- \ нейных и сложных линейных систем. Предполагает применение ЭВМ. Исследуем устойчивость нелинейных систем методом В. М. Попо-. ва и рассмотрим метод гармонической линеаризации, позволяющий вы- ,, явить автоколебания системы и определить их амплитуду и частоту. ?■ 10.4 Особенности устойчивости нелинейных систем Понятие устойчивости для нелинейных систем значительно сложг нее, чем для линейных. Это объясняется тем, что процессы в нелинейных системах имеют ряд существенных особенностей. Линейные системы имеют единственное состояние равновесия, которое может быть устойчивым или неустойчивым в зависимости от структуры и параметров системы. В нелинейной системе может быть несколько состояний равновесия. Например, в следящей системе с сельсинами в качестве элемента сравнивания (рис. 1.14, а) имеется два состояния равновесия: 6 = 0° и 6 = 180° (6 — угол рассогласования системы); состояние 6 = 0° может быть устойчивым или неустойчивым, а состояние 6= 180° является неустойчивым. В нелинейных системах, как и в линейных, возможно появление периодических колебаний, однако в нелинейных системах эти колебания могут быть устойчивыми (автоколебания). Таким образом, для нелинейных систем необходимо различать два понятия устойчивости: устойчивость состояния равновесия и устойчивость автоколебаний. Устойчивость состояния равновесия и устойчивость автоколебаний в нелинейных системах зависят не только от структуры и параметров, но и от начальных отклонений системы относительно состояния равновесия. На рис. 10.4, а, б показаны кривые возможного изменения отклонения 0 (t) нелинейной системы. Если начальное отклонение 60 не превышает величины а и процесс затухает (кривые 1), то состояние равновесия 0 = 0 устойчиво. Если начальное значение 0О превышает величину а и процесс расходится (кривые 2), то состояние равновесия 0 = 0 неустойчиво. Величина а является границей устойчивости но начальному отклонению. В зависимости от ее значения различают: •тойчивость «в малом» — система устойчива, если она устойчива только при малых начальных отклонениях (кривые 1, рис. 10.4, с, б); устойчивость «в большом» — система устойчива (неустойчива) «в большом», если она устойчива при больших (конечных по величине) начальных отклонениях (кривые 2, рис. 10.4, а, б); устойчивость «в целом» — система устойчива «в целом», если она устойчива при любых больших (неограниченных по величине) начальных отклонениях. Как видно из рис. 10.4, а, б, состояние равновесия нелинейных систем может быть устойчивым «в малом» и неустойчивым «в большом». На рис. 10.4, в показан случай, когда состояние равновесия 0 = = 0 системы неустойчиво «в малом». Из рисунка видно, что оба процесса стремятся к колебаниям с одной и той же амплитудой а и частотой: система будет иметь устойчивые автоколебания с амплитудой с. На рис. 10.4, г приведен случай, когда система имеет одно состояние равновесия 0 = 0 и два состояния колебаний с постоянными амплитудами а и flx. Из рисунка видно, что система устойчива «в малом» по отношению к состоянию равновесия 0 = 0. При наличии начальных отклонений, превышающих величину а, процессы стремятся к автоколебаниям с амплитудой ах. Автоколебания существуют «в большом» (при 0О > а). Периодические колебания с амплитудой а являются неустойчивыми. В нелинейных системах могут быть и более сложные процессы. Например, могут возникать автоколебания различной амплитуды и частоты, соответствующие различным начальным отклонениям. Таким образом, в отличие от линейной одна и та же нелинейная система при различных начальных условиях может совершать разные движения. Устойчивая линейная система после снятия воздействия возвращается в исходное состояние. Такая устойчивость называется асимптотической (или устойчивостью в точке). В нелинейных системах, кроме асимптотической устойчивости, может быть устойчивость в некоторой области (неасимптотическая устойчивость), характеризующаяся возвратом системы в определенную область после снятия воздействия. 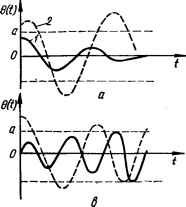 т а О Bit) Of 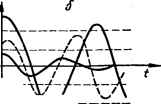 Рис. 10.4. Зависимость устойчивости состояния равновесия и автоколебаний нелинейной системы от начального отклонения 60: о. б — состояние равновесия в = 0 устойчиво «в малом» н неустойчиво «в большом»; в — состояние равновесия в = 0 неустойчиво, автоколебания с амплитудой а устойчивы; г — состояния 6 = 0 устойчиво «в малом», автоколебания с амплитудой а устойчивы «в большом» Рис. 10.5. Нелинейная характеристика у = F (х). В релейной системе (см. рис. 10.3) возникновение этой области объясняется зоной нечувствительности. Асимптотическую устойчивость системы «в целом» для нелинейностей, принадлежащих к определенному классу, называют абсолютной устойчивостью равновесия. К этому классу относятся нелинейные характеристики у = F (х), имеющие любое очертание, но не выходящие за пределы заданного угла arctg k (рис. 10.5). Этот класс нелинейностей охватывает характеристики подавляющего большинства исполнительных элементов систем автоматического управления. 10.5. Частотный критерий абсолютной устойчивости равновесия В. М. Попова Исследование абсолютной устойчивости может быть выполнено при помощи второго метода Ляпунова. Однако более просто эта зада- 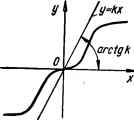 ча решается с помощью связанного с ним предложенного румынским ученым В. М. Поповым. Рассмотрим нелинейную систему, состоящую из устойчивой линейной части с передаточной функцией К (р) и одного безынерционного нелинейного элемента с однозначной характеристикой у = F (х) (рис. 10.6). Пусть в передаточной функции линейной частотного метода, Рис. 10.6. Структурная схема нейной системы. 0 ... 100 101 102 103 104 105 106 ... 143 |












