Раздел: Документация
0 ... 101 102 103 104 105 106 107 ... 143 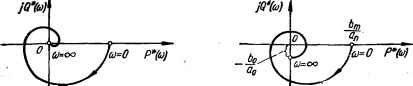 I aI б Рнс. 10.7. Вид преобразованной АФЧХ системы: а — п — m > !; б — п — m => 1. части К(р) = £> (p)IF (р), где D{p)=*b0p™ + blPm-i+ ... + ,/>+& ; (P) = o0pn + Gijon-1 + +an-ip + an, многочлен F (p) имеет все корни в левой полуплоскости или, кроме них, не более двух корней находятся в начале координат (имеют нулевые значения). Иначе говоря, допускается, чтобы в выражении F (р) коэффициент ап = 0 или ап = 0 и ап~\ = 0, т. е. кроме статической система может быть астатической первого или второго порядка астатиз-ма. Пусть нелинейность у = F (х) имеет любое очертание, не выходящее за пределы заданного угла arctg k (см. рис. 10.5), т. е. при любом х 0 < F (х) < kx. Приведем критерий Попова без доказательства. Представим комплексную передаточную функцию линейной части системы в алгебраической форме i№) =/>(«>)+ №(©).(lo.i) Представим, что вместо нелинейного элемента включен линейный элемент с коэффициентом усиления k. В этом случае КПФ системы в разомкнутом состоянии Кр О) - ЩО) = k[P(со) + jQ(со)].(10.2) В соответствии с критерием устойчивости Найквиста-Михайлова для устойчивости замкнутой системы необходимо, чтобы АФЧХ (10.2) не охватывала точку (—1J0). Этот критерий можно сформулировать по другому: для устойчивости замкнутой системы необходимо, чтобы АФЧХ (10.1) не охватывала точку [—(Ilk), j0]. Введем теперь преобразованную КПФ линейной части К* (/со) - Р* (со) + IQ* (со),(10.3) где Р* (со) — Р (со), Q* (со) — coQ (со), т. е. К* (]<а) отличается от К (/ю) только мнимой частью. Заметим, что если п — т > 1, то АФЧХ К* (/ ) имеет такой же вид, что и АФЧХ К Ою) (рис. 10.7, а). Если же п — т = 1, то АФЧХ К* (ja>) при со = со заканчивается на отрицательной части мнимой оси (рис. 10.7, б). Критерий устойчивости В. М. Попова формулируется следующим образом: для абсолютной устойчивости равновесия системы с устойчивой линейной частью и одним безынерционным нелинейным элементом* Рнс. 10.8. Преобразованные АФЧХ нелинейных систем: а, б — состояние равновесия абсолютно устойчиво: в, е — системы не обладают абсолютной устойчивостью состояния равновесия. характеристика которого лежите секторе (0, arctg k), достаточно, чтобы на плоскости преобразованной АФЧХ К* (j<o) через точку I—(Ilk), j0] можно было провести прямую (прямую Попова) так, чтобы преобразованная АФЧХ К* (ja>) линейной части лежала справа от этой прямой. На рис. 10.8, а, б показаны случаи выполнения критерия абсолютной устойчивости, а на рис. 10.8, в, г — случаи, когда системы не обладают абсолютной устойчивостью состояния равновесия. Выше рассмотрен случай, когда характеристика нелинейного элемента находится в определенном секторе и коэффициент k имеет конечное значение. Если нелинейная характеристика располагается во всем первом (и третьем) квадранте, то, согласно рис. 10.5, имеем k~ со. Поэтому точка [—{ilk), jOl будет совпадать с началом координат и для абсолютной устойчивости состояния равновесия системы прямая Попова должна проходить через начало координат. 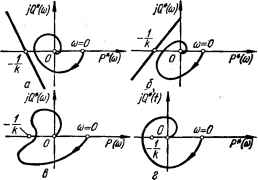 Пример 1. Исследовать абсолютную устойчивость состояния равновесия 6=0 нелинейной системы, структурная схема которой изображена на рис. 10.9. Определить значение k, при котором возможна абсолютная устойчивость. В соответствии с рис. 10.9 комплексная передаточная функция линейной части klK.c Г2(/со)2 + 2Г/со+1 :Я(ш) + ;<г(ш), (10.4) где р.Мох(1-Г*Пл ,п к1ко.ЛТо> г{е>) (1 7aa)8)8 + 4g2ra©a Ч( (1 — ТЧ>*)* + 4gsT2coa * Преобразованную КПФ линейной части К* (/со)получим, умножив мнимую Q (со) (10.4) на со: где Р*(ю)=- K*(M = P*(a)+]Q*(<o), (10.5) (1 — 7,2соа)а + 4272сй2 Q*(w) = (1 — Г2ш2)2 + 4£аГ!<ва Преобразованная АФЧХ К* (/со), построенная в соответствии с выражением (10.5), изображена на рис. 10.10. Из рисунка видно, что АФЧХ К* Ою) линейной части лежит в нижней части полуплоскости и что можно провести к ней касательную 1 в начале координат под углом а0 к вещественной оси, т. е. tg а0 = Q* (со)/Р* (со) 1 тс = = 2\Т.  Рис. 10.9. Структурная схема нелинейнойРнс. 10.10. Преобразован- системы (к примеру).ная А.ФЧХ нелинейной системы (к примеру). Поскольку преобразованная АФЧХ К* (/со) лежит справа от касательной (прямой Попова) и касательная проходит через начало координат, то система обладает абсолютной устойчивостью равновесия при k = со. Естественно, при конечных значениях к система также обладает абсолютной устойчивостью, так как в этом случае через любую точку [—(1/fe), /0] можно провести прямую Попова, лежащую левее преобразованной АФЧХ (например, прямую 2 на рис. 10.10). 10д>. Метод гармонической линеаризации Сущность метода заключается в замене нелинейного элемента системы эквивалентным линейным, который одинаково с нелинейным элементом преобразует гармоническое колебание и характеризуется эквивалентным комплексным коэффициентом усиления. Такая замена позволяет исследовать нелинейные системы частотными методами. В частности, с помощью частотного метода можно выявить наличие автоколебаний, исследовать их устойчивость и определить их амплитуду и частоту, а также решать задачи коррекции нелинейной системы. Основы метода гармонической линеаризации (метода гармонического баланса) разработаны академиками Н. М. Крыловым и Н. Н. Боголюбовым. Применительно к теории автоматического управления этот метод развит Л. С. Гольдфарбом и Е. П. Поповым. В иностранной литературе метод гармонической линеаризации называется методом описывающей функции. Эквивалентный комплексный коэффициент усиления нелинейного элемента При подаче на вход линейного элемента с КПФ К (jo) = N (со) е(е>) синусоидального колебания Хвх = A sinco/, комплексное изображение которого Хвх = Аеы, на его выходе, как известно, возникает также синусоидальное колебание, но отличающееся от входного по амплитуде и фазе хвь,х = К (/со) Аеш - N (со) АеЛаН0а.(10.6) В случае нелинейного элемента выходная и входная величины связаны между собой нелинейной зависимостью *ВЫх = /(Хвх).(Ю.7) Нелинейная зависимость (10.7) может иметь самый различный характер. Предположим, что нелинейная зависимость определяется релейной 0 ... 101 102 103 104 105 106 107 ... 143 |












