Раздел: Документация
0 ... 104 105 106 107 108 109 110 ... 143 Полученные выражения для q (А) и Ъ (А) в нормированной форме имеют вид (Ш.15) b(Ala) = -k0—(\-m), где k0 = В/а. Графики q (Ala) и b (Ala) представлены на рис. 10.14, е. Выражения (10.14) и (10.12) для однозначной релейной характеристики с зоной нечувствительности получаются как частный случай из приведенных формул для q (Ala) и Ъ (Ala) при т = 1. Аналогично можно определить эквивалентные комплексные коэффициенты усиления и для других типов нелинейностей. Коэффициенты гармонической линеаризации и соответствующие графики для некоторых однозначных нелинейных характеристик приведены в табл. 10.1." Годограф вектора нормированного эквивалентного комплексного коэффициента усиления нелинейного элемента В общем случае К0 (А/а) определяется следующим выражением: К0 (А/а) => q0 (А/а) + jb0 (А/а)(10.16) или Ко (А/а) = N0 (А/а) емл/а\(10.17) где iV0 (А /а) = Vql (Ala) + b\ (Ala) — модуль нормированного эквивалентного комплексного коэффициента усиления нелинейного эле--мента Ко (А/а), % (Ala) = arctg- аргумент К0 (А/а). (10.18) Поскольку для нелинейных элементов, имеющих неоднозначную характеристику с петлей гистерезиса, аргумент % (А/а) Ф 0, то первая гармоника выходного колебания элемента сдвинута по фазе относительно колебания на входе. Для естественных нелинейностей (см., например, рис. 10.11, рис. 10.14, формулу (10.15)) всегда Ь0 (А/а) < 0, поэтому они вносят запаздывание колебаний по фазе, что приводит к уменьшению запаса устойчивости системы. Как видно из формул (10.16) и (10.17), К0 (А/а) является комплексным числом и геометрически представляет собой вектор. Поскольку модуль No (Ala) и аргумент % (А/а) этого вектора являются функциями относительной амплитуды А/а, то при изменении А/а конец вектора К0 (А/а) будет описывать кривую — годограф (рис. 10.15). Годограф вектора Ко (А/а) называется нормированной эквивалентной амплитудно-фазовой характеристикой (АФХ) нелинейного элемента. Он позво- 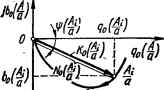 о W 0,637 Рис. 10.15. Возможный вид годографа нормированного эквивалентного комплексного коэффициента усиления К0 (Ala) нелинейного элемента. Рис. 10.16. Годограф вектора Кв (Ala) нелинейного элемента с однозначной характеристикой (рис. 10.13, а). ляет определять амплитуду и фазу первой гармоники на выходе нелинейного элемента в зависимости от амплитуды входного колебания. Параметром годографа является относительная амплитуда А 1а. Эквивалентную АФХ можно строить в декартовой и полярной системах координат. При построении характеристики в декартовой системе координат по вещественной оси накладывают значения q0 (Ala), а по мнимой — ]b0 (Ala), как. показано на рис. 10.15. На этом же рисунке показано построение амплитудной характеристики в полярной системе координат. В качестве примера построим годограф вектора К0 (А/а) релейного элемента с однозначной характеристикой и зоной нечувствительности (рис. 10.13) в соответствии с формулой (10.14). Поскольку в рассматриваемом случае Ь0 (А/а) = 0, то годограф вектора К0 (А/а) совпадает с вещественной осью (рис. 10.16). Он занимает участок вещественной оси от 0 до 0, 637 соответственно при Ala = 1 и А/а = ]2. Каждой точке годографа соответствуют два значения Ala. Эквивалентные АФХ типовых нелинейных элементов приводятся в литературе [57, 67]. Рассмотренный метод гармонической линеаризации является довольно простым и распространенным методом исследования нелинейных систем. Его универсальность состоит в том, что он применим к самым разнообразным нелинейностям. Однако следует иметь в виду, что метод гармонической линеаризации является приближенным методом исследования. Его недостаток состоит в том, что он не дгйэт возможности количественно оценить погрешность, которая получается в результате отбрасывания высших гармоник. Эту погрешность можно оценить лишь качественно: чем выше порядок линейной части системы, т. е. чем более строго выполняется гипотеза фильтра, тем эффективнее в ней будут подавляться высшие гармоники и тем с большим правом имеется возможность ограничиться рассмотрением только первой гармоники выходного колебания нелинейного элемента. 10.7. Исследование устойчивости автоколебаний нелинейных систем методом гармонической линеаризации Благодаря методу гармонической линеаризации становится возможным применение частотных методов для исследования нелинейных систем. Наиболее хорошо разработанными являются частотные методы исследования устойчивости автоколебаний — метод Л. С. Гольдфарба, являющийся аналогом амплитудно-фазового критерия устойчивости, и метод Е. П. Попова, основывающийся на критерии устойчивости Михайлова. Задача исследования устойчивости автоколебаний методом Гольдфарба упрощается, если пользоваться логарифмическими частотными характеристиками. Ниже решается задача выявления возможных автоколебаний, исследования их устойчивости, определения амплитуды и частоты автоколебаний применительно к системе с одним безынерционным нелинейным элементом методом ЛЧХ. Исследование автоколебаний методом логарифмических частотных, характеристик Предварительно структурную схему системы преобразуют так, что все линейные элементы объединяют в линейную часть с комплексной передаточной функцией Кл (/со) и систему представляют в виде последовательного соединения нелинейного элемента НЭ и линейной части ЛЧ (рис. 10.17). Нелинейный элемент заменяют эквивалентным линейным с эквивалентным комплексным коэффициентом усиления •k0K0 (Ala). Общая комплексная передаточная функция нелинейной системы в разомкнутом состоянии Кр (/со, Ala) = k0K0 (Ala) К„ (/со). Предположим, что замкнутая нелинейная система находится на границе устойчивости и в ней имеют место незатухающие колебания. АФЧХ разомкнутой системы в этом случае, согласно амплитудно* фазовому критерию устойчивости, должна проходить через точку с координатами (—1, /0), т. е. Кр (/со, А/а) — —1. Отсюда условие существования в замкнутой системе колебаний имеет вид k0K0 (А/а) Кл (/со) = — 1 .(10.19) или k0K„№ = Z0(A/a)t(10.20) где Z0 (Ala) = — (l/K0 (Ala)). Левая часть уравнения (10.20) является комплексной передаточной функцией линейной части системы с учетом нормирующего множителя k0 нелинейного элемента, а правая — выражением, обратным нормированному ЭККУ нелинейного элемента. Записывая в показательной форме левую и правую части выражения (10.20): k0K„ (/а>) = 0 ... 104 105 106 107 108 109 110 ... 143 |












