Раздел: Документация
0 ... 8 9 10 11 12 13 14 ... 143 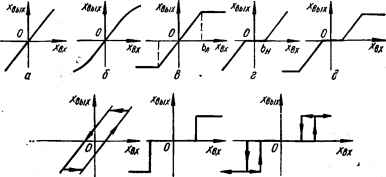 еж Рис. 1.18. Статические характеристики элементов: о — линейная; б — з — нелинейные. 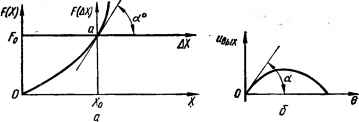 Рис. 1.19. К линеагУнзацни функций: а — F <х) = kxH б — ивых (6) = k sin в. Пример 2. Выходное напряжение сельсинной пары, работающей в трансформаторном режиме, определяется нелинейной синусоидальной функцией «вых (6) = = k sin G, где G — угол рассогласования между роторами сельсина-датчика и сельсина-приемника. График функции показан иа рис. 1.19, б. Если сельсины в качестве измерительного элемента применяются в следящей системе, где в установившемся статическом режиме обычно G = 0, то разложение нелинейной функции в ряд Тейлора необходимо произвести в точке, соответствующей началу координат, 60 = 0, ывых = 0: "вых (6) = «ВЫХо + Д аЪ /е=е„А6- Учитывай, что «вых0 = 0 н что (d«Bblx (0)/d6)e=6o = (kd sin 6/d6)e=6o = tg a = = k (cos G)e=H = k, получим ывых (G) = МО, или, обозначая ДО через в: ивых (G)= = kQ. Последнее выражение является уравнением прямой, касательной к исходной кривой в начале координат. Как видно из приведенных примеров, геометрически при линеаризации криволинейные характеристики заменяются прямыми, касательными к ним в исследуемой точке. При линеаризации нелинейные функции, имеющиеся в дифференциальных уравнениях, разлагаются в ряд Тейлора и члены выше первой степени отбрасываются. Метод линеаризации применим в случае, если нелинейная функция F в окрестности исследуемой точки является непрерывной и к кривой, изображающей функцию, можно провести здесь касательную. Метод линеаризации неприменим, если нелинейная функция F имеет разрыв непрерывности в исследуемой точке, так как при этом частные производные отсутствуют и нельзя провести касательную или составить ряд Тейлора. ГЛАВА 2 Динамические характеристики звеньев и систем автоматического управления В следящих системах (рис. 1.14, а) при повороте ведущего вала на некоторый угол приемный вал также поворачивается на этот же угол. Однако приемный вал занимает новое положение не мгновенно, а с некоторым запозданием после окончания переходного процесса. Переходный процесс может быть апериодическим (рис. 2.1, с) и колебательным с затухающими колебаниями (рис. 2.1,6). Возможно, что колебания приемного вала будут незатухающими (рис. 2.1, в) или возрастающими по амплитуде (рис. 2.1, г). Последние два режима являются неустойчивыми. Каким образом данная система будет отрабатывать то или иное изменение задающего или возмущающего воздействия, т. е. каков характер переходного процесса системы, будет ли система устойчивой нли неустойчивой — эти и подобные вопросы рассматриваются в динамике систем, автоматического управления. 2.1. Динамические звенья автоматических систем Необходимость представления элементов автоматических систем динамическими звеньями. Определение динамического звена Для определения динамических свойств автоматической системы необходимо иметь ее математическое описание, т. е. математическую модель системы. Для этого следует составить дифференциальные уравнения элементов системы, с помощью которых описываются происходящие в них динамические процессы. При анализе элементов автоматических систем выясняется, что разнообразные элементы, отличающиеся назначением, конструкцией, принципом действия и физическими процессами, описываются одинаковыми дифференциальными уравнениями, т. е. являются сходными по динамическим свойствам. Например, в электрической цепи и механической системе, несмотря на различную их физическую природу, динамические процессы могут описываться аналогичными дифференциальными уравнениями. 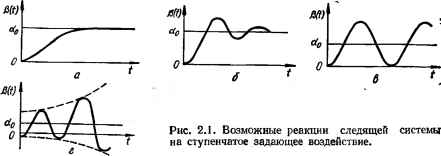 В теории автоматического управления элементы автоматических систем с точки зрения их динамических свойств представляют с, помощью небольшого числа элементарных динамических звеньев. Под элементарным динамическим звеном понимается математическая модель искусственно выделяемой части системы, характеризуемая некоторым простейшим алгоритмом (математическим или графическим описанием процесса). Одним элементарным звеном иногда могут быть представлены несколько элементов системы или наоборот — один элемент может быть представлен в виде нескольких звеньев. По направлению прохождения воздействия различают вход и выход и соответственно входную хвк (t) и выходную xBb,x (/) величины звена. Выходная величина звена направленного действия не оказывает влияния на входную величину. Дифференциальные уравнения таких звеньев можно составлять отдельно и независимо от других звеньев. Поскольку в САУ входят различные усилители, обладающие направленным действием, САУ обладает способностью передавать воздействия только в одном направлении. Поэтому уравнение динамики всей системы можно получить из уравнений динамики ее звеньев, исключая промежуточные переменные. Элементарные динамические звенья являются основой для построения математической модели системы любой сложности. Классификация и динамические характеристики звеньев Тип звена определяется алгоритмом, в соответствии с которым происходит преобразование входного воздействия. В зависимости от алгоритма различают следующие типы элементарных динамических звеньев: пропорциональное (усилительное), апериодическое (инерционное) t колебательное, интегрирующее и дифференцирующее. Каждое звено характеризуется следующими динамическими характеристиками: уравнением динамики (движения), передаточной функцией, переходной и импульсной переходной (весовой) функциями, частотными характеристиками. Такими же динамическими характеристиками оцениваются и свойства автоматической [системы. Рассмотрим динамические характеристики на примере апериодического звена, 0 ... 8 9 10 11 12 13 14 ... 143 |












