Раздел: Документация
0 ... 120 121 122 123 124 125 126 ... 177 1у(х) -+ 4-х3 -9-х2 + 8-х-5 dx у(х):=4х3-9х2 + 8х-5 Находим уравнения касательной и нормали по приведенным выше формулам: tang(x) := у0 + у(хп}(х - хп) погш(х) :=у0 - jjj (* " *ч) tang(x) V* I - 5-х Строим график (рис, 11.2). norm(x) —I 1 + -х 2Ё,
Рис. 11.2. Кривая с касательной и нормалью {из-за неравного масштаба осей график несколько искажен, поэтому угол между касательной и нормалью кажется меньше 90) Столь элементарно уравнения для нормали и касательной можно найти лишь в случае явно зада!шой кривой. Если же кривая описывается неявным уравнением, разделить переменные в котором невозможно, или же ее задает система параметрических уравнений, то построение нормали и касательной значительно усложняется. Покажем на примере, как можно решить задачу такого рода. Пример 11.12. Написать уравнение касательной, имеющей общую точку с кривой при х=1. Кривая задается следующими параметрическими уравнениями: 3t 3 -12 х =- у=- , + t3. + Начнем мы решение этой задачи с того, что зададим хну как функции oit: хМ--".y0):»-г 1 + tI + tJ Ь математическом анализе доказывается, что если функция Y-f(x) задана парамегрически с помощью уравнений к=х{1) Hy-y(t), где x(L),y(t) — дифференцируемыефункции, то производная Y нох находится по следующей формуле (естественно, чтп п роил под г гая от x(t) не должна быть равна 0): 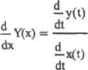 Используя данную формулу, залаем функцию про из водной: 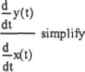 3*3 -1+2-t-1 + 2-Г Нам нужно построить касательную в точке х-1. Но кривая задана парамегрнческимн уравнени-iiMii. зависящими от t. От t зависит н функция производной. Следовательно, лам нужно найти, какое t соответствует х, равному 1. Для этого следует решить уравнение х(с}**1. Проще это сделать аналитически: R: solve, I -1.879.5 [ float, 5 .34735-6-4.1 J Итак, мы получили три корня, два из которых комплексные. Естественно, что t может быть только действительной, поэтому первой мыслью будет отбросить комплексные корни. Однако обратите внимание на то, что порядок мнимой части корней находится на уровне точности расчета. А может, ее существование обусловлено только погрешностью? Чтобы проверить это предположение, увеличим точность до HI знаков (заменив значение в нравом маркере оператора float). Прн этом порядок мнимой части в первом корне уменьшится до уровня 10", в третьем же корне она исчезнет вовсе. Это означает, что мнимая часть — это действительно просто погрешность, возникающая прн пересчете аналитических выражений н десятичные дроби. Следовательно, учитывать ее не нужно. Чтобы избавиться от мнимой части, используем функцию Re. выделяющую из комплексного числа действительную часты Н :*R Мы получили три значения t. соответствупише х- L. Но как такое возможно? Очень просто. Параметрически заданные функции могут иметь несколько точек для одного значения аргумеггга, что исключено в случае явно заданных функций. Собственно, поэтому для описания сложных кривых и применяют параметрическую форму уравнений. Таким образом, наша кривая имеет три точки для x«t. Убедиться в этом можно, построив график. Следовательно, мы должны найти три уравнения касательных (в качестве неременной непользуем г. так как выше уже была задана функция с именем х): tangl(z) :-y(tl) + Ytt>(*~<tJ))tang2(z) :=y(t2) + YOHz - *(tZ)) tang3(z) :«y(t3) + У„(Ш-(г-х<Ь)) Приближенно находим, какой вил будет иметь каждое уравнение: tangl(2) float,3 -»1.14+ 395-z tang2(z) float,3 -> -.742- 1.14-2 tang3(z) float,3 -t- -395+ .742-2 Строим графики кривой и касательных (рис 113). 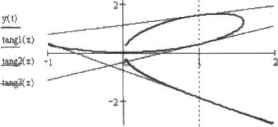 Рис. 11.3. Параметрическая кривая и касательные к ней 11.2.2. Построение касательной плоскости и нормали к поверхности Одной из самых интересных областей применения частных производных является решение задач аналитической геометрии. В любом практикуме по высшей математике есть примеры на нахождение касательных плоскостей и нормалей к Поверхностям, л также касательных линии н нормальных плоскостей к пространственным линиям. Ввиду наличия готовых формул данные задачи довольна просты с математической точки зрения. Однако их решение зачастую связано с подсчетом большого количества частных производных и сложных определителей, поэтому в чисто вычислительном плане они могут быть крайне трудоемкими. Значительную часть работы при решении таких задач может взять на себя Mathcad. В этом под]одделе мы покажем, как решаются задачи подобного типа на примере построения касател ыюй плоскости и нормали к сфере. Сложность задач на нахождение уравнений касательной плоскости и нормали очень сильно зависит от того, уравнениями в какой форме застается поверхность. Если поверхность описывается явным (например, параболоид z(x,y)mxx*-y3) или неявным (к примеру, шар x+y+z-R1) уравнением, то рассчитать уравнения касательной плоскости и нормали несложно даже на бумаге. Однако задача становится на порядок труднее, если поверхность описывает система параметрических уравнений. А так как наиболее интересные поверхности обычно задаются только в параметрической форме, то подобные задачи че являются редкостью. В Mathcad же параметрическая форма описания поверхностей является основной, так как зачастую только исходя из нее можно строить качественные графики. В нижележащем примере показано, как можно найти уравнении касательной плоскости и нормали для параметрически заданной поверхности. Если вы разберетесь с данным примером, то вы с легкостью сможете решать задачи, в которых поверхность описывается явным или неявным уравнением. Пример 11.13. Имеется сфера с радиусом R=5 и центром в начале координат. Построить касательные плоскости, проходящие через точки сферы, которым соответствуют значения аргументов х=2, уЗ, а также нормали к этим точкам Сферу можно пписать неявным уравнением х+у+х-кЛ Однако работать с таким уравнением и Mat head неудобно. Решать поставленную задачу мы будем, задав сферу параметрическими уравнениями: 0 ... 120 121 122 123 124 125 126 ... 177 |












