Раздел: Документация

0 ... 122 123 124 125 126 127 128 ... 177

Аналогично получаются уравнения нормали для агорой точки. В целях экономии места приводить соответствующие формулы не будем.

Строим шар. касательные плоскости и нормаль (рис. П.4) (чтобы понять, как была нарисована линия нормали, перечитайте раздел гл. 6. посвященный функции CreateSpace).

(i.y.ij .21,22, CieateSpncofftomil ,-0,0.3.100)

Рис. 11.4. Шар, касательные плоскости и нормаль к нему

11.2.3. Дифференцирование сложной функции

Дифференцируемая функция U(vf v2, v3... v) называется сложной, если ее аргументы в свою очередь являются функциями некоторых независимых переменных: vl-f(x(,Xj х ... хр[1). Очень часто на практике возникает задача нахождения частных производных сложной функции но переменным, от которых зависят ее аргументы. Например, перед вами может стать задача дифференцирования функции, заданной в сферической системе координат, по переменным X, у, z. В любом задачнике есть примеры на перевод оператора Лапласа или оператора градиента из декартовой системы координат в цилиндрическую и сферическую системы. Подобного рода задачи требуют весьма объемных математических выкладок и хорошей техники вычислений — поэтому стоит использовать MaLhcarJ для их решения.

Рассмотрим функцию, заданную в сферической системе координат. Она зависит от грех переменных, каждая из которых в свою очередь является функцией декартовых координат

U = fU4x,y,z), 9(х, у, Z), ф(х.у, z)) Частные производные U по х, у, г можно найти пп следующим формулам:

й

— и = Эх

е

— и

(ХК j

а

—и

Up )

Эх )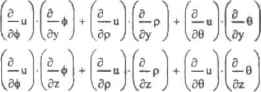

---

ЙУ 3

— и

Эх

То есть чтобы найти частную производную сложной ф\ нкннп но одной из независимых переменных, нужно вычислить произведения частных производных этой функции по промежуточным аргументам и частных производных промежуточных аргументов по независимым переменным, а затем сложить их.

Решение неэлементарных задач на дифференцирование сложной функции требует активного использования возможностей символьного процессора. Однако нужно помнить, что они весьма ограничены, поэтому, к примеру, найти в пару действия лапласиан для сферической системы координат вряд ли получится. Запомните несколько советов, которые позволят вам проводить аналитические расчеты в Mathcad более эффективно.

□Не обращайте внимания на сообщения об ошибках. Еслн формула стала красной, это ие значит, что она не будет вычислена. Просто среда разработки настроена на синтаксис численных расчетов, поэтому ее «смущает», если, например, функция задается без скобок с аргументами после имени. Также сообщение об ошибке появляется, если в выражении присутствуют не заданные численно переменные, хотя аналитический процессор «умеет» отлично работать с такими выражениями.

□Можно работать лишь с реальными, а не абстрактными объектами. К примеру, нельзя проводить аналитические преобразования, оперируя некоей гипотетической, обобщенной функцией, как это обычно делается прн выводах на бумаге. Функция должна быть задана как конкретная зависимость, иначе символьный процессор с ней работать не будет. Аналогично, нельзя оперировать «пустыми» операторами дифференцирования или отдельными дифференциалами.

□Применяйте уникальные идентификаторы, еслн одна и та же величина выступает в разных ипостасях. Поясним этот принцип на примере. В приведенные выше выражения для частных производных сложных функций по независимым переменным входят произведения, в которых промежуточный аргумент сначала фигурирует, как переменная, а затем как функция. Для человека разница ролей, которые исполняет в данном случае промежуточный аргумент, очевидна. Однако машина лишена интеллекта! Для нес величина — это или переменная, или функция. Поэтому, чтобы использовать данные формулы в Mathcad, промежуточный аргумент как переменная и как функция должен иметь различные идентификаторы (например, х и X или у и у)-

Для примера мы решим довольно сложную с вычислительной точки зрения задачу: найдем лапласиан для функции, заданной в сферической системе координат, при условии, что известна лишь формула оператора Лапласа для декартовых координат:

Ли

а2 Зх

а2

ду дх

Оператор Лапласа довольно активно используется в физике. В частности, он входит в гамильтониан — оператор полной энергии, поэтому задачи, подобные решаемой ниже, не редкость в классической и особенно квантовой механике, Уравнение Лапласа также применяется для описания полей со сферической симметрией.

---

Пример 11.14. Найти лапласиан функции и(р, 9, ф)=ра-81п(в)сов(ф) в сферической системе координат

Начнем мыс того, что зададим саму функцию и:

и := р sin (е).сов(Ф)

Далее введем выражения, связывающие декартовы координаты х, у, г со сферическими координатами р. 6, ф:

X:=p-sin(9)COsfa) У:=р-яЬ(еУзш(ф) Z:=p-cos(e)

. L \я обозначения декартовых координат мы использовали буквы в верхнем регистре. Это необходимо, чтобы система могла «различить» случаи, когда они выступают ках неременные (при этом мы будем обозначать их символами в нижнем регистре) и как функции от сферических координат.

Функцию и(р, В.ф) мы можем представить как сложную, а которой промежуточными аргументами являются р, 9, ф. а независимымп переменными - х. у. г. Используя приведенные выше формулы, мы найдем частные производные ti(p. в. ф) по декартовый координатам. Повторное дифференцирование полученных фунюшй как сложных даст входящие в выражение лапласиана частные производные второго порядка по х, у и г.

Итак, в первую очередь мы должны представить сферические координаты как функции от координат декартовых. Для начала попробуем объединить уравнения, их связывающие, в систему и решить ее с помощью оператора solve относительно р, в и ф. Однако полученный при этом результат окажется мало приемлемым, так как » нем будет использоваться функция atan2, не имеющая аналогов в «бумажной» математике. Следовательно, выразить р, в и ф через х, у и z мы должны самостоятельно.

Чтобы найти выражение для р, возведем вес три уравнения в квадрат и сложим их:

XYZ2 simplify -» р Таким образом, г зависит от декартовых координат следующим образом:

, Гг 2 2

р := J, х + у + г

Так как идентификаторы г как переменной н ках функции от х, у. г должны различаться, мы использовали обозначение «p».

Формулу для ф легко найти, разделив выражение для у на выражение для х:

Y . ... sinfo) Xcos W

Отсюда:

0

Формулу для 9 находим, выразив данную переменную из выражения для Z (учтя полученную ранее формулу для р):

0 ... 122 123 124 125 126 127 128 ... 177