Раздел: Документация
0 ... 26 27 28 29 30 31 32 ... 177 таких как, например, функции вычисления матричных норм илн сортировки элементов векторов по возрастанию. Функции этой группы можно найти в разделе Vector and Matrix (Векторные и матричные) списка Insert Function (Вставить функцию), И, наконец, к Третьему типу матричных вычислений следует отнести те задачи, решить которые можно только используя возможности системы программирования Mathcad. Например, только написав соответствующую программу, можно просуммировать элементы вложенного массива. В этой главе мы рассмотрим все возможные операции с матрицами, исходя из принципа <от простого к сложному», по прежде чем рассматривать особенности решения матричных задач, разберемся, как матрицы создаются И редактируются. 3.1. Создание матриц и извлечение из них данных Массивом (Агтау) называется любая упорядоченная последовательность элементов, адресуемых посредством целочисленных индексов. В качестве элементов массива могут использоваться числа, строки н другие массивы. Огромным достоинством Mathcad является то, что массивы в нем отображаются в традиционном для математики представлении в виде прямоугольных таблиц - матриц. Исходя из структуры, все массивы Mathcad могут быть разделены на три большие группы. □Векторы (Vectors). В Mathcad этим термином принято обозначать матрицы-столбцы, хотя иногда под ним понимают и матрицы-строки (что особенно характерно для нашей математики), □Матрицы (Matrices). Двумерный* массив. Представляет собой множество элементов, организованных по принципу шахматной доски. □Тензоры (Nested Arrays). Так называемые вложенные массивы. Матрицы или векторы, элементы которых также являются массивами. Если же разделять массивы по пршщипу особенностей задашь их элементов, то можно выделить две группы. □Векторы, матрицы или тензоры, при задании когорых не существует прямой связи между величиной элемента и его индексами. □Ранжированные переменные (range variables). Векторы, величина элементов которых напрямую определяется индексом. Пример 3.1. Типы массивов 11Л Vector := 2 Mairix:= 1 2 3 1. Tenzor - 4> 4 5 6 V7 8 9j Массив является основным элементом, на основе которого строится практически любая программа или численный алгоритм. Учитывая это, совсем не удивительно, что в Mathcad можно реализовать целых восемь способов задания массивов. □ Задание матрицы или вектора вручную с помощью команды Insert Matrix (Вставить матрицу). 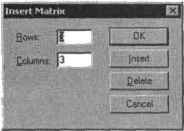 Рис. 3.2. Окно Insert Matrix (вставить матрицу) Чтобы открыть панель Matrix (Матрица), можно также воспользоваться сочетанием клавиш Ctrl+M или соответствую щей командой меню Insert (Вставить). Параметры создаваемой матрицы можно определить в окошках Rows (Строки) и Columns (Колонки). Прн этом количество элементов будущей матрицы не может превышать 100, Реально же в Mathcad можно работать с массивами любой объективно встречаемой прн расчетах размерности. Данное же ограничение связано с тем, что заполнять вручную матрицы с числом элементов, большим 100, нецелесообразно — для этого используются некоторые другие методы из приведенного выше списка. Определившись с размерами матрицы, нажмите 0К (или Enter). При этом в документ будет вставлена заготовка с черными маркерами вместо элементов. Последовательно перемещая курсор с помощью мыши или клавиш управления курсором, введите в маркеры нужные значения (рис. 3.3). Элементы матрицы можно представить и символически: как В виде переменкой, так и в виде выражения. m.itriMЕЗ
Рис. 3.3. Заполнение матрицы значениями На практике обычно оперируют не матрицами, а их именами. Эта связано с тем, что, во-первых, многие преобразования можно провести только с помощью имен, а во-вторых. □Определение матрицы последовательным заданием каждого элемента. □Использование ранжированных переменных. □Задание с помощью языка программирования. □Применение встроенных функций. □Через связь с другим приложением, например Excel. □Создание таблицы данных. □Чтение из внешнего файла. Наиболее простым способом задания матрицы является использование специального окна Insert Matrix (Вставить матрицу) (рис. 3.2). Чтобы его вызвать, нажмите на панели Matrix (Матричные) одноименную кнопку с изображением квадратной матрицы с маркерами вместо элементов. очень важной может оказаться задача экономии места документа, что особенно актуально в случае больших матриц. Чтобы вместо матрицы использовать ими, нужно определить ее как значение некоторой переменной. Делается это точно так же, как при задании переменной как числа: введением матричной заготовки с помощью окна Insert Matrix (Вставить матрицу) в маркер оператора ириснаивания. Элементы матрицы могут быть как числами, так И проками или выражениями. Правила их определения при этом сохраняются те же, что и при задании простых переменных и функций. То есть если среди выражений или символов, выступающих в качестве элементов матрицы, есть неизвестные или параметры, то они должны обязательно быть численно определены выше. В птютивном случае матрица должна быть задана как функция. В случае определения элементов матрицы строковыми выражениями их текст обязательно должен быть взят в кавычки. Пример 3.2. Задание матриц с элементами-переменными и элементами-функциями а:= I Ь:=2 М : = 2 2 К* + о а - Ь V 0.667 -2 J { sin(x+у) соь(х-у) Л N(x,y). ainjj + y) co>(j-y)jV7j -I2 4 2 -I 2 1-3 2 Есть только одно принципиальное отличие между определением значений переменных (или функций) и элементов матрицы — непосредственно в матрицу нельзя добавить матрицу (о том, как задаются тензоры (вложенные матрицы), мы поговорим ниже). В случае необходимости можно добавить к уже созданной и заполненной матрице строку или столбец. Чтобы это сделать, поставьте курсор к тому элементу, правее которого должен быть введен столбец (или ниже которого — в случае строки). Одним из описанных выше способов откройте окно Insert Matrix (Вставить матрицу), в окошках параметров которого введите 0 — для строк и 1 - ДЛЯ столбцов (иди ггаоборегт - в случае добавления строки). Нажмите Enter, В случае заданной матрицы всегда можно пилучить значение любого ее элемента, используя его матричные индексы. Матричные индексы равняются номеру строки и столбца, на пересечении которых элемент находится. В нашей математике отсчет строк и столбцов принято начинать с t, В программировании же начальные индексы обычно равняются 0. По умолчанию в Mathcad строки и столбцы также отсчитываютсЯ с 0. В том случае, если такая система вам неудобна или непривычна, вы можете изменить точку отсчета индексов на 1 (или любую другую). Чтобы это едьлать, откройте окно Worksheet Options (Параметры рабочего листа) меню Tools, на вкладке Built-in Variables (Системные переменные) внесите соответствующие коррективы в величину параметра ORIGIN 0 ... 26 27 28 29 30 31 32 ... 177
|
||||||||||||||||||
