Раздел: Документация
0 ... 27 28 29 30 31 32 33 ... 177 (Точка отсчета). Впрочем, можно поступить и проще, сделав переопределение данной системной переменной инерху документа:( ORIG[N:=l Однако, даже если вы привыкли к отсчегу строк и столбцов с единицы, лучше все-таки используйте примятые по умолчанию правила. Это даст преимущества хотя бы в том, что вы лучше будете понимать примеры из справочной системы и алгоритмы других пользователей. Итак, чтобы получить значение какого-то матричного элемента, нужно ввести имя матрицы с соответствующими индексами и поставить *—* (или, если элемент задан символьным выражением, *—>*). Для задания индексов па панели Matrix (Матричные) имеется специальная кнопки Subscript (Индекс), которой соответствует клавиша <[*. Нажав ее, вы увидите, что на месте будущего индекса, чуть ниже текста имени матрицы, появится черный маркер. В него через запятую следует ввести значения индексов. На первом месте при этом должен стоять номер строки, а на втором — столбца. При выделении элемента вектора нужно задать юл ько индекс строки. Вообще, индексы могуг быть определены и через выражения или специальные функции. В том случае, если элементы матрицы заданы как функции, то извлечены они должны быть в таком же виде. Пример 3.3. Выделение элементов матрицы * 1 г\ { "Vector" V:= VQ = "Vector" vt = 0 M ;= 2J f sin(x+ y) cos(x-y) ") N(x,y);= SLH M 0,0 M 0,1 M 1,0 0.5 N(x.y)00-N(71,671)0,0 cos--у sm(x + y) Аначогично извлечению отдельных элементов матрицы, используя индексы, можно задать новую матрицу. Для этого просто нужно проделать операцию присвоения для каждого элемента по отдельности. При этом размерность матрицы будет определяться элементом с наибольшими индексами. В том случае, если вы присвоите значения не всем элементам создаваемой матрицы, вге остальные будут автоматически определены как 0. Пример 3.4. Поэлементное задание матриц Ми0:=2 М -сэ M0J:=I М1.Г=3 N- N„ л := "Starr 0,0 N. "End" 2.1 ("Start" 0 и "End" ) Кстати, переопределяя значения элементов матриц, можно производить их редактирование. Oco6eimo важен этот способ в случае больших массивов, не .отображаемых на мониторе, а также при создании различного рода программ. Пример 3.5. Форматирование матрицы переопределением элементов V:=(l 2 3 4) V0,0:="Slait" 0,3 "End" V-< "Start" 2 3 "End" ) Поэлементное задание — единственный способ определения тензоров (вложенных массивов) в Mathcad. Чтобы задать тензор, просто присвойте соответствующим элементам основного массива значения в виде матриц или векторов (иди, что тоже возможно, других вложенных массивов). При этом совершенно не обязательно, чтобы все элементы тензора были определены как матрицы. При желании можно создать массив, содержащий данные всех типов. Пример 3.6. Поэлементное задание тензора 0,0 1.0 .(1 2) "Tenzor" Т 0.1 1.1 о т = 3.142> {2,1}; ОД) . Tenzor" Соответствующие матрицы тензора можно задать выше в виде переменных, а в качестве элементов тензора прописать их имена. Пример 3.7. Альтернативный способ задания тензора аг=(1 2)br=jt с := "Tenzor" d := а b d Т = ( Ш з t Tenzor" 3.142Л (2,1 J Внимательно изучив приведенные примеры, вы обнаружите, что при визуализации тензоровMathcad отображает не сами элементы-матрицы, а цифры, отражающие их размерность, заключенные в фигурные скобки. В большинстве случаев такой подход вполне оправдан в связи с тем, что обычно вложенные массивы изучаются не напрямую, а извлечением нужных элементов. Однако иногда все же бываег полезно раскрыть тензор. Чтобы это сделать, обратитесь к уже хорошо нам знакомому окну Result Format (Формат результата). Здесь, на вкладке Display Options (Параметры отображения) установите флажок Expand Nested Arrays (Раскрывать вложенные массивы). При этом все тензоры будут визуализированы в развернутом виде. Так, вложенный массив примера 3.7 приобретет следующий вид: Т = (12) 3.142 1 Извлечь матрицу тензора можно точно так же, как элемент простого массива. Столь же просто можно узнать значение любого элемента его вложенной матрицы. Для этого следует просто использовать два набора индексов: первый должен соответствовать положению самой матрицы, второй — ее выделяемому элементу, Единственной тонкостью при этом является то, что выражение, соответствующее матрице, следует обязательно взять в скобки. Пример З.В. Выделение элементов матриц тензора ГО 2) (3 4) Т1.0 = <6 4>Т1,1=(2) Помимо одного элемента, можно очень просто выделить и целые матричные столбцы. Чтобы это сделать, нужно использовать специальный оператор панели Matrix (Матричные) Matrix Column (Столбец матрицы) (также вводится сочетанием Ctrt+б), В том случае, если требуется выделить строку, матрицу необходимо транспонировать (оператор Matrix Transpose (Матричное транспонированне) той же рабочей панели). Пример 3.9. Выделение из матрицы строки и столбца 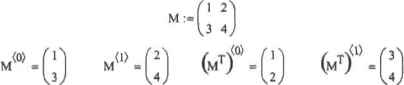 4 3.1.1. Ранжированные переменные Одной из разновидностей задания массивов является использование так называемых ранжированных переменных. Ранжированная переменная (от англ. range - ряд) - это разновидность вектора, особенностью которого является непосредственная связь между индексом элемента н его величиной. В Mathcad ранжированные переменные очень активно используются как аналог программных операторов цикла (например, при построении графиков). Простейшим примером ранжированной переменной является вектор, значение элементов которого совпадает с их индексами, Для задания такой ранжированной переменной выполните следующую последовательность действий. 1.Введите имя переменной и оператор присваивания. 2.Поставив курсор в маркер значения переменной, нажмите кнопку Range Variable (Ранжированная переменная) панели Matrix (Матрица). При этом будет введена заготовка в виде двух маркеров, разделенных точками: 0 ... 27 28 29 30 31 32 33 ... 177 |












