Раздел: Документация
0 ... 8 9 10 11 12 13 14 ... 87 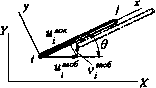 Введем две прямоугольных системы координа, локальную х, у, связанную со стержневым элемец том, и глобальную x, y. Так как элемент положен вдоль оси х локальной системы коорд наг, то н перемещения его концов uj лок и uf* ЛОк Рис.2.8 произойдут вдоль той же оси (перемещения vj и V / в направлении оси у равны нулю). В глс. бальной системе координат им соответствуют смещения Щ ..глоб глоб ..глоб ..глоб j » Определим связь между перемещениями узлов i и j в локальной и глобально) лок .лок системах координат, т. е. между uj и uj , с одной стороны, и uj „глоб „глоб vj и Vj , с другой (рнс. 2.8). Из геометрических представлений можно записать: ,глоб „глоб > п . глоб . п г. coso + vl sino = \l т глоб~\ лок глоб V. = —И- sind + vf*06 cosd = [-m I где / = COS 0,ТП — sin 0, или в матричной форме: глоб Здесь Т 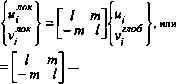 {лок \глоб 1 матрица трансформации. (2.12) (2.13) Для обоих узлов элемента: лок лок vj Iтп ОО -mI ОО ОО Iтп О0 -тпI глоб ui глоб vi глоб "j глоб , или и"" - Ты1*"6, где Т= т О о f Аналогично преобразуются и приложенные к узлам силы: (2.1* (2.1Я 2.2.3.2. матрица жесткости Ранее составленная система уравнений равновесия (2.11) для рассматриваемого эл? мента справедлива также и для локальной системы координат. В принятых здесь обознЗ чениях система уравнений (2.11) записывается следующим образом: eat j Л
Добавляя в систему еще два уравнения, чтобы включить две новые составляющие перемещений, получим: еа l 10-10 0 0 0 0 -10 10 0 0 0 0 ЛОК "i лок vi лок и1 лок vj ft о лок С учетом (2.14) н (2.15) это уравнение можно переписать: k*°" Т и = Tf. Умножая обе одсти этого равенства на Г и учитывая, что Т* Т= I, получим: ТткжжТи=/.(2.16) Таким образом, матрица жесткости к элемента в глобальной системе координат может быть записана следующим образом: к=Т1кжжТ.(2.17) Она представляет собой симметричную матрицу размером 4x4. В развернутом виде матрица жесткости к выглядит следующим образом: еа l
(2.18) Остается вычислить направляющие коэффициенты через начальные координаты узлов стержневого элемента: х.-х,y. - yi i = cos в = —--, m = sin0 = —- ll (2.19) 2.2.3.3. Напряжения Напряжение в произвольно ориентированном стержневом элементе вычисляется по формуле; <т = ее = еъ ЛОК "i ЛОК и1 = е 1 i l l глоб глоб 7 m о от О О i тпи2»06! j глоб ИЛИ ? более краткой форме (индексы «глоб» в данном случае опущены): <т =—[-/ — тп I m\ UJ (2.2; Рассмотрим несколько примеров, 3 2.2.3.4. Примеры Пример 1. Плоский кронштейн состоит нз двух одинаков; стержней длиной L (рнс. 2.9). Площадь поперечного сеч; ния стержней А, модуль упругости материала Е. Крщ штейн нагружен силами Р н Р, как показано на рисущ. Определить: а) смещение узла 2; б) напряжения в каждо стержне. Решение: А. Исследуемую конструкцию кронштейна мода моделировать двумя стержневыми элементами 1 н 2, щ показано на рнс. 2.9. В локальных координатах обоих элементов: ЕА кГ = к2"ж-- Эти две матрицы не могут быть связаны вместе потому, что они составлены для эд: ментов, расположенных в различных координатных системах. Поэтому их необходш перевести в глобальную координатную систему AT. Для элемента 1: в = 45® ; I = тп = -j~2/2. С учетом (2.17) получаем матрицу жесткости для элемента 1 в глобальных коордии 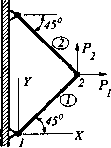 Рис.2.9
к,= Т к/ Для элемента 2: 6 = 135®; l = —42~j2; ТП = ~j~2~/2. Матрица жесткости для элемента 2 в глобальных координатах: "2 V2 Щ V? 1 -1-11 ЕА -1 1 1~1 2L ~1 1 1 -1 1 ~1 ~1 1 Уравнения равновесия для системы конечных элементов: k2=Tjk?™T2 0 ... 8 9 10 11 12 13 14 ... 87 |












