Раздел: Документация
0 ... 5 6 7 8 9 10 11 ... 87 е i
(1.18) где щ — перемещение i-ro узла всей системы. В (1.18) учтено, что усилие р приложено в узле 3, а усилие fj (реакция опоры) — в узле 1. Узел 2 свободен от внешних нагрузок. Теперь следует наложить граничные условия в перемещениях, а именно: Uj = 0. Это достигается замещением 1-й строки и 1-го столбца нулями и помещением ив главную диагональ любого числа, отличного от нуля: 10 0 о aj+a2 -а2 i о -а2 а2
Решением этой системы лииейиых алгебраических уравнений является: U, =0; Ы, = р1 еа, из=- р1 1 Л +— \А1 (1.19) 2) Глава 2 Типы конечных элементов. Стержневой и балочный элементы. Линейная задача 2.1. Типы конечных элементов 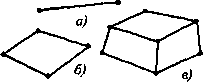 Рис.2.1 Существует большое количество разнообразных типов конечных элементов ( программе ANSYS — около 100). На рис. 2.1 показаны лишь некоторые из них. Задача разбиения тела на конечны элементы неоднозначна. В некоторы) случаях (например, в случае расчет) ферм) конструктивные элементы тако вы, что совпадают с конечными эле ментами. Так, всю ферму можно моде лнровать линейными стержневыми эле ментами (рнс. 2.1 а). Такими же эле ментами можно моделировать различ ного рода упругие конструктивные эле менты (пружины, стержни, тяги н т. п.] а также системы трубопроводов. В этих случаях моделирование конструкции не пред eras ляет особого труда н состоит в выполнении некоторого объема работы по стандартны) правилам. Гораздо сложнее выполнить эту операцию для двумерных или трехмерны; областей. Здесь, прежде всего, нужио выбрать тип (или типы) конечных элемента! (например, рнс. 2.1 б, в), наилучшим образом аппроксимирующие исследуемую область Плоские двумерные элементы (рнс. 2.1 б) применяются, в основном, для моделирован» мембран, тонких пластин, тонкостенных оболочек н т. п. Объемные трехмерные элемент! (рнс. 2.1 в) применяются, в основном, прн исследовании полей температур, деформацм напряжений в массивных телах н т. п. На приведенном выше рнс. 2.1 все элементы имеют прямые стороны, а помещены на концах элемента (рнс. 2.1а) или в вершинах углов (рнс. 2.1 б, в). Так! образом, каждый элемент (или его сторона) ограничен соседними узлами и вся обла< будет аппроксимирована линейными элементами. Это наиболее простые элеме Напомним, что значение искомой функции в узлах считается известным. Соответствующий этому элементу аппроксимирующий полином (функция элемента), определяемый по значениям функции в узловых точках элемента, будет линейным, т. к. он будет строиться по двум точкам. Можно образовывать элементы с числом узлов вдоль одной стороны более дв; (рнс. 2.2). В этом случае введение одного или нескольких дополнительных узл< позволяет сделать стороны элементов криволинейными. Такие элементы являются бол< точными, т. к. функции элементов будут строиться уже не по двум, а по трем (рнс. 2.2 а, I или четырем (рнс. 2.2 в) точкам н, следовательно, будут являться полиномами второй ил третьей степени. 2.1.1. Линейный упругий элемент. Матрица жесткости Начнем подробное рассмотрение типов конечных элементов с модели одного из пр стейших типов — упругого линейного элемента (например, упругой пружины), схема к< торого приведена на рнс. 2.3. D а) б) Рис.2.2 Элемент ограничен двумя узлами, обозначенными как I и j . В этих узлах приложены силы fl и fj [щ, соответственно. Эти силы ft вызывают смещения узлов щ и uj [м] (илирис 2.3 [.*<*]) Элемент характеризуется жесткостью к : [Ц/м], т. е. силой, необходимой для его деформации иа единицу длины. Таким образом, зависимость силы от деформации запишется как fj = к а, где а = Uj — U- (удлинена элемента). При этом удлинение равно разности перемещений концов элемента Uj — U.). Принято, что сила положительна, если ее направление совпадает с поло-ельиым направлением оси х. (Рассмотрим силы, действующие в узлах данного элемента: вузле/: f. = k(И, -И .) ; вузле/: f} = k[uj -и.), то же в матричной форме: к -кЛ\иЛ и, -к к и I J) /л •, или Au = Г (2.1) Здесь к—матрица жесткости; и — вектор смещений; f — вектор сил. Заметим, что матрица жесткости к — симметричная матрица. 2.1.2. Система упругих элементов. Матрица жесткости системы элементов Рассмотрим систему из двух последовательно соединенных упругих элементов, схема >рой приведена иа рис. 2.4. и f 1 1 «2>F2 u3f3 рис.2.4 Для элемента 1, согласно (2.1), можно записать: *7 Гк1 v7 И- Аналогично для элемента 2: *2 "*2 ~*2 *2 J 0 ... 5 6 7 8 9 10 11 ... 87 |












