Раздел: Документация
0 ... 2 3 4 5 6 7 8 ... 87 4)приложение к модели граничных условий (закрепление на границе или граничные нагрузки); 5)численное решение системы уравнений (автоматически); 6)анализ результатов. Этапы 1, 2, 3, 4 относятся к препроцессорной стадии, этап 5 — к процессорной стадии, этап 6 — к постпроцессорной стадии. Построенная модель делится на конечные элементы достаточно простой формы. Имеются несколько типичных форм конечных элементов, в которых поле смещений определяется по смещениям узлов с помощью некоторых интерполяционных функций. По вычисленным таким образом смещениям определяются поля напряжений и деформаций. Наиболее трудоемкий этап решения задач с помощью МКЭ — это создание конечно-элементной модели на стадии препроцессорной подготовки (preprocessor), т. к. автоматическое построение сетки элементов не гарантирует от появления ошибок. Правильное приложение нагрузок н граничных условий также представляет определенные трудности. Пятый из перечисленных выше этапов (численное решение системы уравнений) выполняется автоматически и, как правило, особых трудностей не вызывает (за исключением систем с плохо обусловленной матрицей жесткости). Шестой этап (анализ результатов) существенно облегчается имеющимися мощными инструментальными средствами визуализации результатов. Учитывая то, что в конечно-элементных задачах неизвестными являются перемещения в узлах, а также то, что в трехмерных задачах каждый узел тетрагонального элемента может иметь перемещения по трем направлениям (рис. 1.8), система уравнений равновесия, записанная в матричной форме, может иметь размерность, достигающую 100000 и более. Однако для современных ЭВМ решение таких систем уравнений — вполне посильная задача. При составлении уравнений равновесия учитывается, что сумма проекций всех сил на каждую нз координатных осей равна нулю, а сумма внутренних сил равна внешней силе с обратным знаком. В трехмерных моделях число узлов обычно больше числа элементов, а число степеней свободы в 3 раза больше числа узлов (за исключением числа кинематических граничных условий). Матрица жесткости [Д] связывает векторы узловых смещений {Щ и нагрузок {F}-Матрица жесткости является симметричной диагональной матрицей, что существенно облегчает ее обработку. Как следует из основной концепции МКЭ, вся модель конструкции (или отдельной ее части) делится на множество конечных элементов, соединенных между собой в вершинах (узлах) (рис. 1.9 а, б). Силы действуют в узлах. Конечный элемент не является «абсолютно жестким» телом. 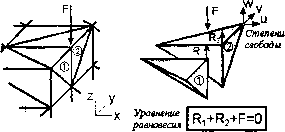 Рис.1.8 1.4.3. Конечные элементы о) 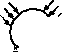 Узлы Элементы 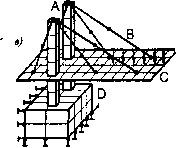 Порядок элементов III III Рис.1.9 Конечно-элементная модель предполагает, что напряжения и деформации имеются и вне данного конечного элемента. Имеются несколько наиболее употребительных типов конечных элементов (рис. 1.9 в): брус (А), стержень (В), тонкая пластина или оболочка (С), двумерное или трехмерное тело (D). Естественно, что при построении модели могут быть использованы не один, а несколько типов элементов. Достоверность расчетов по МКЭ зависит от многих факторов, в том числе и от количества конечных элементов. Однако, если напряжения не меняются значительно в пределах модели, то количество конечных элементов несущественно влияет на точность вычисления напряжений. Конечные элементы могут быть линейными (элементы первого порядка) или параболическими (элементы второго порядка) (рис. 1.10). Линейные элементы имеют прямые стороны и узлы только в углах. Таким образом, минимальное число узлов трехмерного элемента равно 4. Параболические элементы могут иметь промежуточный узел вдоль каждой из сторон. Именно благодаря этому стороны элемента могут быть криволинейными (параболическими). При равном количестве элементов параболические элементы дают большую точность вычислений, т. к. они более точно воспроизводят криволинейную геометрию модели и имеют более точные функции формы (аппроксимирующие функции). Однако расчет с применением конечных элементов высоких порядков требует больших компьютерных ресурсов и большего машинного времени. Рассмотрим самый простой трехмерный линейный элемент с 8 узлами (рис. 1.11). Каждый из узлов имеет 3 степени свободы. Это означает, что необходимо рассмотреть 24 узловые смещения и столько же узловых сил. Таким образом, размерность матрицы жесткости [к], связывающей вектор узловых смещений с вектором узловых сил, будет [24 х 24]. Компоненты матрицы жесткости обратно пропорциональны модулю упругости. Таким образом, нулевой модуль упругости означает отсутствие конечного элемента (Рос. 1.12). В этом случае деление на нулевой модуль упругости приведет к значительным погрешностям. Бесконечно большой модуль упругости означает, что данный элемент является абсолютно жестким. Кроме того, если теория упругости допускает бесконечные напряжения (например, в вершине трещины), то в МКЭ напряжения всегда конечны. Несколько замечаний относительно соотношения между сторонами элемента. «Длин-Чые» элементы с соотношением сторон 2 и более (рис. 1.13) можно использовать, если не Рис. 1.10 ожидаются большие градиенты смещений, деформаций и напряжений, т. е. вдали от зоны действия концентраторов напряжений. Смещения Сшил 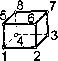
Матрица жесткости Рис. 1.11 Модуль упругости Е Б = <ю Е = 0 I Возможно Неправильно Рис. 1.12 Ь/ау2 Возможно Плохо  Рис.1.13 Рис.1.14 Если конструкция и нагрузки симметричны относительно оси, как показано, например, на рис. 1.14, задача может быть решена с помощью плоских симметричных конечных элементов. 1.4.4. Построение сетки конечных элементов Одним из наиболее важных этапов в конечно-элементном анализе является построение на модели сетки нз конечных элементов, т. е. разделение всей модели на маленькие кусочки (конечные элементы), связанные между собой в узлах. В программном комплексе ansys имеется два основных метода построения сетки: построение произвольной сетки (рис. 1.15 а) и построение упорядоченной сетки (рис. 1.15 6). Произвольная сетка строится автоматически, при этом соседние элементы могут существенно отличаться по размерам (рис. 1.15 а). Упорядоченная сетка строится путем деления геометрических элементов модели иа некоторое число частей (рис. 1.15 б). В автоматически построенных сетках с большим числом элементов число узлов преобладает над числом элементов. Отношение между узлами и элементами, примерно, 2:1 для плоских произвольных сеток и 6:1 для произвольных трехмерных сеток с четырехгранными элементами. Очевидно, что чем меньше линейный размер конечного элемента Л (рис. 1.16), тем большее количество элементов в модели, при этом время вычислений экспоненциально возрастает, а ошибки анализа уменьшаются. Однако, ошибки уменьшаются не до нуля, т. к. с увеличением числа элементов накапливаются ошибки округления в ЭВМ. Практика расчетов с применением МКЭ позволяет дать следующие рекомендации (рис. 1.17): 1) линейные элементы требуют более частой сетки, чем квадратичные элементы (с одним промежуточным узлом) или кубичные (с двумя промежуточными узлами); 2) упорядоченная сетка (б) является более предпочтительной, чем произвольная сетка (а); 0 ... 2 3 4 5 6 7 8 ... 87 |












