Раздел: Документация
0 1 2 3 4 5 6 7 ... 87 1.3.4. Уравнения равновесия Согласно теории упругости, напряжения в элементе объема должны удовлетворять следующим уравнениям равновесия: Э<т„ 9 г -+-+fx=0. (1.15) Эх ху 2* да. + ду Jy n*fxfy- объемная сила (например, сила тяжести) на единицу объема. 1.3.5. Граничные условия Граница S тела может быть разделена на две части (рис. 1.6): S и S . Тогда гра- ничные условия можно записать как: U = М, V = V на 5 ; и t =t , X X t = t на S , У У t где t ,t х у (i.i6) заданные силы (или напряжения) на участке границы S, И,V — заданные смещения на участке границы S (кинематические граничные условия). В МКЭ все виды нагрузок (распределенные поверхностные нагрузки, объемные силы, сосредоточенные силы и моменты н др.) приводятся к сосредоточенным силам, действующим в узлах. х Рис.1.6 1.4. Идея и область применения метода конечных элементов. Основные этапы практической реализации 1.4.1. Основные понятия Возникновение МКЭ связано с решением задач космических исследований (1950 г.). Этот метод возник из строительной механики и теории упругости, а уже потом был осмыслен математиками, которые часто называют данный метод вариационно-разностным, подчеркивая тем самым его математическую природу. Они занимаются математическим обоснованием МКЭ, т. е. проводят теоретический анализ его сходимости и точности результатов. Представители же инженерного направления решают довольно сложные технические задачи, часто не задумываясь над строгим обоснованием применяемых нми приемов, а построенные алгоритмы и программы проверяют на известных точных решениях. Существенный толчок в своем развитии МКЭ получил после того, как было доказано (1963 г.), что этот метод можно рассматривать как один из вариантов известного в строительной механике метода Рэлея—Ритца, который путем минимизации потенциальной энергии позволяет свести задачу к системе линейных уравнений равновесия. Связь МКЭ с процедурой минимизации позволила широко использовать его при решении задач в других областях техники. Метод применялся к задачам, описываемым Уравнениями Лапласа или Пуассона (например, электромагнитные поля). Решение этих Уравнений также связано с минимизацией некоторого функционала. Известны решения с помощью этого метода задач распространения тепла, задач гидромеханики и, в частности задач о течении жидкости в пористой среде. Область применения МКЭ существенно расширилась, когда было показано (1968 г.) что уравнения, определяющие элементы в задачах строительной механики, распростра иения тепла, гидромеханики, могут быть легко получены с помощью таких вариантов ме тода взвешенных невязок, как метод Галёркина или способ наименьших квадратов. Уста новление этого факта сыграло важную роль в теоретическом обосновании МКЭ, т. к. по зволило применять его при решении многих типов дифференциальных уравнений. Такш образом, метод конечных элементов из численной процедуры решения задач строитель ной механики превратился в общий метод численного решения дифференциальных урав нений или систем дифференциальных уравнений. Этот прогресс был достигнут за доволь но короткий срок, благодаря совершенствованию быстродействующих ЭВМ. Более подробно история возникновения и прикладная теория МКЭ изложены в рабо тах[1-8]. Кратко изложим сущность МКЭ и основные этапы его практической реализации. Основная идея метода конечных элементов состоит в том, что любую непрерывнук величину (перемещение, температура, давление и т. п.) можно аппроксимировать моде лью, состоящей из отдельных элементов (участков). На каждом из этих элементов иссле дуемая непрерывная величина аппроксимируется кусочно-непрерывной функцией, кото рая строится на значениях исследуемой непрерывной величины в конечном числе точе> рассматриваемого элемента. В общем случае непрерывная величина заранее неизвестна, и нужно определить зна чения этой величины в некоторых внутренних точках области. Дискретную модель, одна ко, очень легко построить, если сначала предположить, что известны числовые значени этой величины в некоторых внутренних точках области (в дальнейшем эти точки мы назо вем «узлами»). После этого можно перейти к общему случаю. Чаще всего при построении дискретной модели непрерывной величины поступаю: следующим образом: 1.Область определения непрерывной величины разбивается на конечное число по добластей, называемых элементами. Эти элементы имеют общие узловые точки и в сово купности аппроксимируют форму области. 2.В рассматриваемой области фиксируется конечное число точек. Эти точки называ ются узловыми точками или просто узлами. 3.Значение непрерывной величины в каждой узловой точке первоначально считаете: известным, однако необходимо помнить, что эти значения в действительности еще пред стоит определить путем наложения на ннх дополнительных ограничений в зависимости oi физической сущности задачи. 4.Используя значения исследуемой непрерывной величины в узловых точках и ту ил» иную аппроксимирующую функцию, определяют значение исследуемой величины внутри области. Поясним сказанное выше на примере исследования распределения температуры е стержне. В общем случае распределение температуры неизвестно, и мы хотим определил значения этой величины в некоторых точках. Методика построения дискретной модели остается точно такой же, как описано выше, но с добавлением одного дополнительного шага. Первоначально считают значения температуры в некоторых точках в пределах стержня известными. Определяют множество узлов и значения температуры в этих узлах, которые теперь являются переменными, т. к. они заранее неизвестны. Область (в нашем случае — длина стержня) разбивается на элементы, для каждого из которых определяете» аппроксимирующая функция. Узловые значения температуры должны быть теперь «выбраны» таким образом, чтобы с учетом граничных условий (например, значений температуры на концах стержня) обеспечить наилучшее приближение к истинному распределению температуры вдоль стержня. Этот «выбор» осуществляется путем минимизации некоторой величины, связанной с физической сущностью задачи. Если рассматривается задача распространения тепла, то минимизируется функция, связанная с соответствующим дифференциальным уравнением. Процесс минимизации сводится к решению систем линейных алгебраических уравнений относительно узловых значений температуры. В прочностных задачах, где определяются поля перемещений, деформаций и напряжений, минимизируется потенциальная энергия деформированного тела. Аппроксимирующие функции чаще всего выбираются в виде линейных, квадратичных или кубических полиномов. Для каждого элемента можно подбирать свой полином, но полиномы подбираются таким образом, чтобы сохранить непрерывность величины вдоль границ элемента. Этот полином, связанный с данным элементом, называют «функцией элемента». С этой точки зрения конструкцию можно рассматривать как некоторую совокупность конструкционных элементов, соединенных в конечном числе узловых точек. Если известны соотношения между силами и перемещениями для каждого отдельного элемента, то, используя известные приемы строительной механики, можно описать свойства и исследовать поведение конструкции в целом. В сплошной среде число точек связи бесконечно, и именно это составляет основную трудность получения численных решений в теории упругости. Понятие «конечных элементов» представляет собой попытку преодолеть эту трудность путем разбиения сплошного тела на отдельные элементы, взаимодействующие между собой только в узловых точках, в которых вводятся фиктивные силы, эквивалентные поверхностным напряжениям, распределенным по границам элементов. Если такая идеализация допустима, то задача сводится к обычной задаче строительной механики, которая может быть решена численно. Таким образом, при использовании МКЭ решение краевой задачи для заданной области ищется в виде набора функций, определенных на некоторых подобластях (конечных элементах). 1.4.2. Основные этапы практической реализации Как было отмечено ранее, согласно МКЭ, модель конструкции сложной формы подразделяется на более мелкие части (конечные элементы) сравнительно простой формы, в пределах которых ищется приближенное решение. Результатом такого моделирования обычно является поле напряжений и смещений в целой конструкции. Таким образом, решение задачи с применением МКЭ состоит из следующих основных этапов (рис. 1.7): ЮхЯ 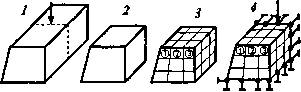 F=5 кЯ © 5 ® <3> д=о [К] {A}=[Kf {F} dv s"dx а - Ее Рис.1.7  Напряжения 100% 80% 60% 40% 20% 0% 1)идентификация задачи, присвоение ей имени; создание чертежа конструкции и нагрузок; 2)создание геометрии модели, пригодной для МКЭ; 3)разбиение модели иа сетку конечных элементов; 0 1 2 3 4 5 6 7 ... 87 |












