Раздел: Документация

0 1 2 3 4 5 6 ... 87

Проверка:

Га ЪТ1\а Ь] 1 \d -bla b] \l О] [cd\ [с dj-faa-bcl-c a\cd\ [о l\

(ad-bc)l

Решение системы линейных уравнений (2.1) в предположении, что матрица А не сингулярная, может быть записано следующим образом:

х-А-Ь

Таким образом, основной задачей при решении системы линейных уравнений является нахождении инверсии матрицы коэффициентов.

Положительно определенные матрицы. Квадратная матрица А размерности (и X и) называется положительно определенной, если для некоторого ненулевого вектора х размерности (и) выполняется условие: хт Ах > 0.

Дифференцирование и интегрирование матриц Для матрицы a(i)= Jfl. . it) j дифференцирование н интегрирование определены следующим образом:

dt

,(t)=

dt

\A(t)dt=[\aij{t)dt\.

1.3. Матричная форма записи основных соотношений теории упругости

В результате воздействия на тело внешних нагрузок и температуры его точки могут переместиться относительно друг друга в новые положения. В этом случае вектор перемещения для трехмерной задачи можно записать следующим образом:

{u}=\ux,Uy,Ugl(1.5)

где U ,U ,U (нли соответственно и, v, и>) — проекции вектора перемещений на коор-х у Z

динатные оси X, у, Z соответственно.

Для двумерной задачи вектор перемещений имеет два компонента:

{и}={их,иу\.(1.6)

Здесь н далее фигурными скобками { ... } будем обозначать вектор-столбец (для

экономии места он будет иногда записываться в строчку). Квадратными скобками [ ... ]

будем обозначать квадратные н прямоугольные матрицы.

Разность перемещений двух соседних точек вызывает деформации в материале н связанные с ними напряжения.

В общем случае, деформации и напряжения в материале конструкции состоят из шести компонентов (рнс. 1.3):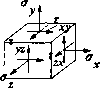

О ,0 ,G ,Х ,Т Л —для напряже-х у z ху yz zxv

Рис. 1.3

НИИ и е ,е ,е ,у ,у ,у х у z ху yz zx

маций.

для дефор-

---

1.3.1. Плоские (двумерные) задачи Под плоским напряженным состоянием понимают случай:

(1.7)

Примером этого может служить плоское тонкое кольцо постоянной толщины, находящееся под действием внутреннего давления (рис. 1.4).

УУУУ

Рис. 1.4Рис. 1.5

плоской деформации говорят в случае:

е2 = гу2=12х=0 К*0)-С»-»)

Примером может служить длинный цилиндр с постоянной площадью сечения под действием постоянного вдоль оси z внутреннего дааления (рис. 1.S). Возможен вариант, в

котором £ = const Ф 0.

1.3.2. Основные соотношения между напряжениями, деформациями и температурой

Для упругих изотропных материалов имеем:

у

1/е -v/e о -v/e 1/е о о о 1/g

1	а
	X		хО
*	а		£ „
	У		уо
-	г . ХУ.		УхуО

или {е }= [е {<т }+{е ),где Eq —начальные деформации, е гости, V — коэффициент Пуассона, g — модуль сдвига. Заметим, что:

е

(1.9)

— модуль упру-

g =

2(l + vY

(1.10)

Анализ (1.10) показывает, что для однородных изотропных материалов существуют Две независимые константы, описывающие механическое состояние материала

Решив систему уравнений (1.9), получим зависимость напряжений от деформаций:

---

Г

7-v

7 v О v 1 О О 0 (l-v)/2

У

хО

>0

(1.11

или { а }= [ Е ]{е }+ { t7fl J, где { GQ )= — [ Е ]{efl J — начальные напряжения.

Приведенные выше формулы справедливы для случая плоского напряженного со стояния. При плоской деформации выражения для постоянных материала в формулах не обходимо заменить на следующие выражения:

ЕV

Е ->-t.v-»-, G->G.(1.12

1-v2 1-v Например, связь между напряжениями и деформациями для случая плоской деформа

кии:

Т

I *У)

Г

(7 + v)(7-2v)

1-v v О v 1-v О

О 0 [l-2v]J2

	f	е X		6х0	\
		е У	• — •	еУо	•
	1	У [ *У.		УхуО	)

(1.11 а

Начальные напряжения вследствие изменения температуры определяются по формуле:

хО

уо

\JxyO

аАТ) \=\оАТ О

(1.13

где О. — коэффициент термического расширения, ЛТ — изменение температуры. Заме тим, что если температурные деформации не стеснены, то при изменении температуры > конструкции не возникают упругие термические напряжения.

1.3.3. Соотношения между деформациями и смещениями Для малых деформаций и смещений имеют место следующие зависимости £ = ди/дх, = bvjby, у = ди/ду + dv/dx, или в матричной форме:

или {е }=[/)]{ и}.(1.14

е X		д/дх	0
е у		0	д/ду
У Vxy)		. д/ду	д/дх

0 1 2 3 4 5 6 ... 87