Раздел: Документация
0 ... 4 5 6 7 8 9 10 ... 87 растягивающих напряжений ......  I Рис. 1.29 (например, как на схеме рис. 1.29), нет необходимости строить подробную сетку элементов вблизи этой точки, т. к. здесь действуют, в основном, сжимающие напряжения. Область максимальных 1.4.6. Точность результатов Численный анализ, к которому относится и МКЭ, требует некоторой идеализации ре. альиой конструкции. Поэтому, несмотря на -мощное развитие вычислительной техники результаты вычислений по МКЭ не свободны от ошибок. Использование вычислительной техники в роли «черного ящика», без понимания основных процессов и этапов вычислений, может привести к существенным ошибкам К сожалению, ие исключены также и ошибки операторов. Приступая к конечно-элементному анализу, инженер должен понять: —к какой области анализа относится данная задача; —какая часть всей конструкции должна исследоваться подробнее; —какие упрощения можно допустить в данной задаче. Естественно, это требует определенной квалификации исследователя. Ошибки могут возникать на различных стадиях конечно-элементного анализа: при постановке задачи, дискретизации (построении модели), численном решении. Ошибки постановки задачи могут возникать, когда выбранный тнп конечных элементов или их размер ие соответствуют физическому поведению материала в конструкции Несколько уменьшить эту ошибку (по крайней мере, ту ее часть, которая связана с размером конечного элемента) можно, используя автоматическое построение сетки. Однако основным источником ошибок при постановке задачи является некорректное задание граничных условий. Таким образом, успех конечно-элементного анализа зависит от точности воспроизведения на модели граничных условий, геометрии и свойств материала натурно? конструкции. Ошибки дискретизации возникают при замене реальной конструкции ограниченны» числом конечных элементов (с учетом их формы н размеров). Ошибки, связанные с численным решением систем уравнений, обычно менее значимы, чем перечисленные выше два типа ошибок. При конечно-элементном анализе, как правило, неизвестными являются смещения, i результатом решения в этом случае будет аектор смещений в узле {и}. Смещения в другш точках элемента вычисляются интерполяцией. После аппроксимации поля смещений (в пределах элемента) соответствующим полиномом, называемым «функцией формы», могут быть вычислены деформации и на пряжения. Описанная схема вычислений показывает, что наибольшая точность достига ется при определеини смещений в узлах. Деформации вычисляются дифференцированием соответствующих смещений, поэто му максимальная точность вычислений деформаций н напряжений будет в центре элемен та. На рис. 1.30 показана деформированная частица для случая чистого изгиба. -1 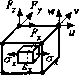
Смещения в уздах Ffl Усилия в уздах М" du *"dx Ди Лх МКЭ Теория Рис. 1.30 Как видим, теоретическое н численное решение совпадает в центральной части конечного элемента. Тип и количество элементов влияют на точность вычислений. Так, например, при вычислении силы в случае нелинейного анализа, при небольшом числе конечных элементов их количество существенно влияет на величину вычисляемой силы Гт*ГтТТП F (рис. 1.31). Однако при увеличении Н43Э£СГ-+-Н 51 чИСла элементов результаты стабилизируются. Существуют два метода конечно-элементного анализа: Л-метод {h — длина стороны конечного элемента) и р-метод (р — порядок полинома аппроксимирующей функции). Для повышения точности решения Л-метод требует увеличения числа элементов. В соответствии с -методом для увеличения точности надо повысить порядок полинома аппроксимирующей функции. Так, например, на рис. 1.32 б элементы более высокого порядка демонстрируют и большую точность результатов по сравнению с линейными элементами (рнс. 1.32 а). 160 8-узловых элементов 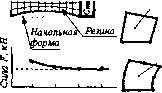 4 16 64 128 Количество элементов, п Рис.131 Линейный 4-х узловой элемент Квадратичный 8-и узловой элемент (лучше/) 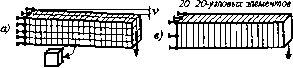 ошибка а9% 20 20-узловых элементов ошибка аЗ% 20 20-узловых элементов б) Г- 9? Щ4
ошибка «12% ошибка я0,5 % Рис.1.32 На точность результатов влияет также и ориентация сторон элементов. Для изгибаемой консольной балки увеличение числа элементов по высоте балки не дает повышения точности результатов (рис. 1.32 в). Гораздо лучшие результаты дает увеличение числа элементов второго порядка по длине балки (рис. 1.32, г). Для получения достоверных результатов в зонах концентрации напряжений размер элементов должен быть меньше. На рис. 1.33 показан Фрагмент растягиваемой полосы с центральным отверстием. Известно, что максимальные напряжения действуют в сечении А —А, поэтому в окрестности данного сечения сетка элементов Должна быть гуще, чем у левой границы полосы.рис j $3 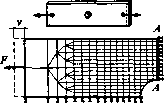 1.4.7. Пример. Растяжение ступенчатого стержня Поясним основные понятия МКЭ на простейшем примере осевого растяжения сту. пенчатого стержня. Данный пример сейчас будет приведен лишь в качестве иллюстрации без подробных объяснений. Объяснение методики работы с системами конечных элемец, тов, соединенных между собой как последовательно, так н параллельно, будет дано t гл.2.
Рис.134 Рис.135 Ступенчатый стержень (рнс. 1.34) с двумя ступенями одинаковой длины / н площадь» поперечного сечения ступеней и жестко заделан с левого торца и нагружен на про тивоположном торце осевым усилием Р. Определить перемещения сечений 1, 2 н 3. Разобьем стержень на два элемента (участка) 1,2 и введем на границах элементов узлы 1, 2, 3, в которых будем отыскивать неизвестные перемещения U. Таким образом ступенчатый стержень будем моделировать двумя последовательно соединенными стер» невымн конечными элементами. Рассмотрим отдельно стержневой элемент, изображенный на рнс. 1.35. Он имее длину /, площадь поперечного сечення А, в узлах приложены усилия н Р, от которых эти узлы имеют осевые перемещения Uj и Запишем для элемента на рнс. 1.3! соотношения, очевидные нз курса сопротивления материалов: Р1=(и1-и21 P2=-f-(U2-Ul) или то же и матричной форме: Е-А I 1 -1 -1 1 или {P}=[Kfu}, (1.11 где Е — модуль упругости материала стержня. Матрица \к\, связывающая между собой в (1.17) узловые усилия н перемещения, не сит название матрицы жесткости элемента. Составим уравнение равновесия для всего стержня, изображенного на рнс. 1.34, объединив соотношения для элементов 1 и 2, записанные с учетом (1.17). Так как стержень се стоит из нескольких элементов, то естественно предположить, что матрица жесткости всего стержня должна включать в себя матрицы жесткости образующих его элементов Как будет показано ниже, для данной задачи главные диагонали матриц жесткости элементов должны совпадать с главной диагональю глобальной (общей) матрицы жесткости всего стержня н состыковываться в узле 2 (см. рнс. 1.34). На основании (1.17) общую систему уравнений равновесия можно записать в виде: [K]{u}={F), 0 ... 4 5 6 7 8 9 10 ... 87 |
|||||||||||||||||||||||||||||||||||||||||||||||












