Раздел: Документация
0 ... 11 12 13 14 15 16 17 ... 87 mmtmt к qL/2 qL/2k qL2/l2qL2/l2 Puc.2.15 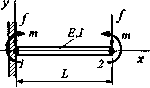 Рис.2.16 Конечно-элементная система уравнений в матричной форме для данной задачи следующая: Е1 ,3 12 6L -12 6L 6L 4L2 ~6L 2L2 -12 -6L 12 -6L 6L 21? -6L 4L2 = м} Щ Зададим граничные условия: vj =в] = 0, F2y = —f, М2 = Ю. Вычеркивая столбцы и строки с номерами 1 н 2, соответствующие нулевым граничным условиям, получим следующую систему уравнений:
m откуда находим перемещения правого конца балки: v4 1 )-2L2f + 3Lm\ \-pL4/8El) [в2] 6EI[-3Lf + 6m J {-pL3/6El\ Из общей системы уравнений равновесия, учитывая (А), получаем реакции опор: F1Y М] EI -12 6L -6L 2L2 (А) (В) Заметим, что уравнение (В) представляет собой суммарные силу и момент, действующие иа брус в узле 1. Помимо реакций опоры они включают в себя узловые силу и мо-Мент. связанные с приведением распределенной нагрузки к узлам. Как видно из рис. 2.12, [ -pL/2 ] составляют: { •. / г • Таким образом, истинные опорные реакции должны быть \-pL2ll2) РРектированы: F1Y Mi f PL/2 1 Г -pL/2 j [5pL2/l2\\-pL2/l2\ pL pL2j2 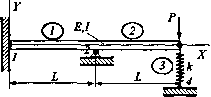 Пример 3. Брус, показанный Рис.2.17 рис. 2.17, жестко закреплен в точке ; имеет шарнирно неподвижную опору j точке 2 и пружинную опору с жестко, стью к в точке 3. Дано: Р = 50 кН, к = 200 кН/ L=3m,Е = 210Щ I = 2У.10-4м 4. Определить смеще. ния, углы поворота и реакции опор. Решение. Для решения задачи применим два балочных элемента / и 2, а также один упр,. гий элемент 3 (рнс. 2.17). На рисунке номера элементов, в отличие от номеров точек, об. ведены. Матрица жесткости упругого элемента 3: к3 = v3 v4 k -k -k k Глобальная матрица жесткости для двух последовательно соединенных балочнщ элементов приведена в примере 1 данного параграфа. Добавим к этой матрице полученную выше матрицу жесткости упругого элемента: £7 тЗ
где k =—k. EI Граничные условия: V; =&j =v2 =vj =0; M2 =M3 =0; F3y - -P В соответствии с граничными условиями вычеркиваем первые три и седьмую cip- и соответствующие столбцы. После этого получаем: тЗ Ш -6L 2L* -6L 12 + k -6L 21f -6L 4If Решая это уравнение, получим смещение и угол поворота в узлах 2 и 3:
PIf El\j2 + 7k)
4
Из глобальной системы уравнений в матричной форме мы получаем реакции опор: -69,78 кН -69,78 кНм 116,2 кН 3,488 кН Расчетная схема балки с вычисленными реакциями опор выглядит 69,78 кН50 кН так, как показано на рис. 2.18. Задача решена полностью. Пример 4. Для рамы, показанной на рис. 2.19 а, известно: Е = 300 ГПа, I = 69,78кНм03х10~4м<. А = 0,44х10~~2м2. 3,488 кН Определить смещение и поворот угловых соединений 1 и 2 , а также опорные реакции. 116,2 кН Рис.2.18 3000 н E.I.A 500 н/м Ф 0 2 Ф 34 8м 2000 н 2666,7н-м 3000 5м 2000 н 2666,7н-м Ф 3 Ф б) 2 Ф 4 Рис.2.19 -&ШЩе- Сначала приведем распределенную нагрузку к узлам, как показано на Pj*0- 2.19 б. В локальной координатной системе матрица жесткости для каждого из трех очных элементов выглядит следующим образом: 0 ... 11 12 13 14 15 16 17 ... 87 |












