Раздел: Документация

0 ... 9 10 11 12 13 14 15 ... 87

	Щ	vy и2	V2	"3	V3
	1	1 -1	-1	0	0~	С 1 "/		Fix
	1	1 ~1	-1	0	0	vy		Fiy
ЕА	-1	-1 2	0	-1	1	"2		F2x
2L	-1	-1 0	2	1	-1	V2		F2y
	0	0 ~1	1	1	-1	"3		F3x
	0	0 1	~1	-1	1	v3.		Ы

Граничные условия:

uj=vj=u3

v3 = 0,F2x=P]tF2y

Вычеркивая 1,2, 5 и 6 столбцы и строки, получим:

ЕА 2L

2 О О 2

"2

Решая эту систему уравнений, получим искомые перемещения в узле 2:

W еа\р2\

Б. Согласно (2.20), получаем формулы для напряжений в обоих стержнях:

[0

°1

Е42 L 2

[-1 -1 1

ХЕАЛ

а2=тт[1

1 -11]

ЕА

0 Pi

{Pi Р2 о о

Задача решена.

ШХШ 2. Для плоской стержневой конструкции, изображенной на рис. 2.10, дано: Р = Ю00 кН, L = 1m. Е = 210ГПа.

(для элементов У н 2),

Q А~ 62x10 4м2 (для элемента 3). "Ределить перемещения и реакции опор.

Г7®Щ£- Составим глобальную матрицу жест-Для всей конструкции. Для элемента У:

и , I = и, ТП — 1. Матрица жесткс-* глобальных координатах: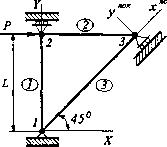

Рис.2.10

---

1

ujVy u2 v2

00 0 0

010-1

00 0 0 0-101

(Н/м).

Для элемента 2: в = 0 1 = 1, тп—Q. Матрица жесткости для этого элемента:

и2 v2 и3 v3

{?10х10д)к,0х10-4) 1

1 0 -1 ООО -1 0 1

(Н/м).

0 0 0 0 Для элемента 3: 0 = 45°; 1=14 = 42/2. Матрица жесткости:

щ vy u3 v3

\?10х109\б2х10-4)

3гт

г2

0,5 Of -0,5 -Oj 0,5 Of -Oj -Of -0,5-Of Oj 0,5 -Oj-0,5 Oj 0,5

(Н/м).

Система уравнений равновесия для всей конструкции:

1260Х105

~0j 0,5 0	0	-0,5	-0,5	Щ		F1X
и о	-1	-0,5	-0J			FjY
1	0	-1	0	"2		?2Х
	1	0	0	V2		F2Y
		1,5	0,5	и3		F3X
(Симм.)			0,5	Уз.		?3Y .

Обращаем внимание на то, что индексы X, Y вектора сил соответствуют глобально* системе координат. Граничные условия:

ufo6 = vfo6 = угюб = 0; улок = 0;

F2X=P,F3T=0.

После преобразования приведенной выше системы уравнений с учетом граничных ус ловнй получим:

vf* =

+ vfo6)=0.

---

..глоб „глоб п Отсюда: и3 -v3 = 0.

Получим также выражение для силы в узле 3: 42 J2

~н3х ~

для учета нагрузки н граничных условий в уравнениях равновесия вычеркиваем 1,2 и 4 строки и столбцы. После этого получим:

	1-1 0	"2		Р
1260x10s	-1 1J 0J	"3		F3X
	0 Oj OJ	УЗ.		F3Y.

Учитывая равенство и3 — Vj = 0, а также соотношение между силами в узле 3, перепишем предыдущее выражение в виде:

1260x10s	1-1 0	и2		Р
	-1 1J 0J	"3		Рзх
	0 OJ 0J	и3.		-рзх.

Из приведенного выше матричного уравнения следует: 1260Х105

1 -1		р
-1 2		Рзх
0 1		~F3X.

Отсюда получаем: F3% = —1260x10s и3. Сложение 2 и 3 строк дает:

" 1 -1

1260x10s

-1 3

Решив эту систему уравнений, получим перемещения:

\и2]1 \ЗР\ \0J0U91 \

и3\ 2520x10s [Р J \0№3968\

(м).

Из глобального конечно-элементного уравнения в матричной форме можно вычислить все реакции опор. Задача решена

2.2.4. Произвольное расположение элементов в пространстве

Аналогично тому, как это делалось в п. 2.2.3 для Цементов, произвольно расположенных на плоско-ти> элементы матрицы жесткости сначала за-, ываются в локальной системе координат х, у, г >Ис-2.П)) а затем трансформируются в глобальную си«ему координат X, Y. Z.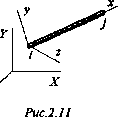

0 ... 9 10 11 12 13 14 15 ... 87