Раздел: Документация
0 ... 38 39 40 41 42 43 44 ... 96 F, F} F3 F4 F} F6 F, F8 F9F, F} Fj F4 F5 F6 F, F8 F9
[AF(a)»]{Ay*F(A)jjJ а)в) kTkT tC tOkT С (С tC tC tC цГСчГСССС i [A»*A(F)»]\ 6) Рис.2.7. Объединение множеств nASj и I7ASj A2(F2) = (a5>a9>>> Л2О5) = (*3»*1())- Кроме того, появились новые тела унитарного цвета Fj (Л), не существовавшего ранее в раскрасках исходных Я -множеств: A(F7) =(а5,а7), A2(F7) =(а5,аи). В результате матрица тел [Аи х A(F)V. ], объединяющая матрицы [AjxA(F)j] и [AjxA(F)j] и новые тела, имеет вид (см. рис.2.76). На основании состава тел A(F)Vj определен состав унитарных цветов FiA) =(FuF2iF3,FA,F5,FG,F7,F8,F9) и сформирована булева матрица [Аи х ЯЛ)] (рис.2.7в). 2.1.4. Особенности полихроматических графов Одним из основных аспектов моделирования сложных систем является отображение различных связей между элементами этих систем, для чего используется аппарат теории графов. Обыкновенным графом G=(A,C) называется упорядоченная пара конечных множеств: множества вершин Л, и множества ребер или дуг, соединяющих вершины графа. Однако традиционный математический аппарат теории графов ие содержит средств одновременного описания и состава, и разнообразных свойств вершин и ребер графа, что сужает возможности моделирования реальных систем. Такие средства содержит аппарат полихроматических графов, основанный на понятиях теории полихроматических множеств. Полихроматическим называется граф nG, вершины и/или ребра которого являются полихроматическими множествами. Способы описания полихроматического графа зависят от характера взаимосвязи цветов вершин и ребер по их влиянию на унитарную раскраску F(G) Яв-графа. Полихроматические множества вершин и ребер Яв-графа имеют вид: ПБЛ =(A,F(a),F(A),[Ax F(a)UA х ЯЛ)],[Л х A(F)]\ (2.162) nSc =(C,F(c),F(C),[C x Яс)],[С x ЯС)],[С х C(F)]),(2.163) где Л, С - множества вершин и ребер, рассматриваемых без учета их раскраски; F(a)f F(c) - множества персональных цветов всех вершин и ребер; Я Л), F(C) - множества унитарных цветов - унитарные раскраски TISA и TISC; [Л х F(a) ], [С х F(c) ] - булевы матрицы персональных раскрасок вершин и ребер; [Л х ЯЛ)], [С х F(C)]~ булевы матрицы цветов вершин и ребер, одноименных унитарным цветам F(A)hF(C); [А х A(F)]f [С х C(F)J - булевы матрицы вариантов тел, обеспечивающих существование унитарных цветов ЯЛ) и ЯО. Если условия существования унитарных цветов множества вершин не зависят от условий существования унитарных цветов множества ребер , то полихроматический граф описывается четверкой компонентов: где С - описание инцидентности между вершинами и ребрами TIG -графа; F(C) - унитарная раскраска TIG - графа, определяемая в виде функции, аргументами которой являются раскраски F(A) и F(C) полихроматических множеств ITSA, ITS с • Такой граф называется ITS -графом с независимой раскраской вершин и ребер. Обычное множество А вершин можно принять как полихроматическое, но с пустым составом унитарных цветов и пустыми составами персональных цветов элементов; точно так же множество ребер С можно принять как полихроматическое, но с пустыми составами унитарных цветов и персональных цветов ребер. Поэтому в любом ЯС-графе можно выделить множества Л и С, определяющие обычный граф G = (Л,С), вершины и ребра которого бесцветны; этот граф называется бесцветным каркасом ЯС-графа. ЯС-граф представляет собой единый комплекс, объединяющий множества TISл вершин и TISC ребер в единое целое. Несмотря на независимость унитарных раскрасок вершин и ребер, при объединении IISд и TISc в единый комплекс их унитарные цвета могут быть по-разному взаимосвязаны в унитарной раскраске F(G). Раскраску F(G) ЯС-графа можно определить как результат теоретико-множественной или логической операции над множествами унитарных цветов F{A) вершин и F(C) ребер по схеме: где F(A)V или F(A)A означает, что данная раскраска принадлежит дизъюнктивному или конъюнктивному множеству вершин, a F(C)V или F(C)A - что данная раскраска принадлежит дизъюнктивному или конъюнктивному множеству ребер ЯС-графа. Примером ЯС-графа с дизъюнктивным IISд - множеством вершин и конъюнктивным IISс -множеством дуг служит структурная модель производственного участка (рис.2.8). В случае F(C) = (F(A),0) полихроматический граф имеет вид ЯС =(С,Я5д), а в случае F(C) =(0,F(C)) имеет вид ЯС = (С, TISq ). IIG=(G,F(G),IISA,IISc), (2.164) 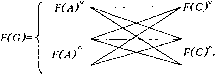 0 0 ... 38 39 40 41 42 43 44 ... 96 |












