Раздел: Документация
0 ... 39 40 41 42 43 44 45 ... 96 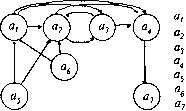 G=(A,C) F1F2F3F4F5F6F7 F8 F9 F10 F„ F„ [AxF(A)] Fq Fio FJi Fq uT С uT С С .ГГТ •Sver • f l1(2) C«3) c1(4) CX3) cx4) cx2) cx4) C4(7) c5(0 C5(2) C<X1) c6(2)
bt(2) c1(3) c1(4) C2(3) C2(4) CX2) cx4) C4(7) c5(1) CX2) c6(1) c6(2)
[C*F(C)] [C*C(F)J Рис.2.8. IJG-траф структурной модели производственного участка. Вершины /7<3-графа: а\ - горизонтально-фрезерный станок; #2 - вертикально-фрезерный станок; а$ - токарный станок; я4 - сверлильный станок; а$ - рабочий; а§ - промышленный робот; a-j - склад деталей. Цвета ЯС-графа (свойства заготовок и деталей): F\ - плоская поверхность; F2 - торец; F3 - наружная поверхность; F4 - круглое отверстие; F5 - фасонная поверхность; Fg - паз прямолинейный сквозной; F7 - паз прямолинейный глухой; Fg - паз криволинейный; Fg - перемещение заготовки (детали); F\q - нежесткая деталь; F1t - вес заготовки Р <15 кг; F12 - вес заготовки 15 < Р < 50 кг Если в раскраске F(G) ЯС-графа унитарные цвета F(А) множества IJSа вершин существуют независимо от унитарных цветов F(C) множества FfSc ребер, то состав унитарных цветов F(G) выполняется по формуле: F(G)=F(A)v F(C),(2.165) а если унитарные цвета F(A) существуют только при наличии одноименных цветов в раскраске F(C) ребер, то F(G) = FU)aF(C),(2.166) /ГС-граф с независимой раскраской вершин и ребер используется при моделировании реальных систем в тех случаях, когда элементы системы являются функционально самостоятельными объектами, свойства которых независимы от других объектов и связей между ними. Вершина ak исключается из состава TISA вершин такого /ГС-графа по методике, изложенной выше. В результате получается измененное множество Я5дk вершин вида (2.77). Если в исходном ЯС-графе существовали ребра, инцидентные исключенной вершине ak, то эти ребра исключаются из состава TISq - При независимой раскраске вершин и ребер добавление в ЯС-граф новой вершины ak рассматривается как включение ak в множество TISд вершин исходного ЯОграфа. Введение ak в TIS А требует также решения вопроса о появлении новых связей между элементами исходного множества вершин и ak , т.е. о добавлении нового ребра или нескольких ребер. К основным операциям над ЯС-графами относятся операции объединения, пересечения и разности ЯС-графов, а также выделение некоторой части ЯС-графа. Содержание этих операций различается для графов с независимой и зависимой раскраской вершин и ребер. Выделение части ЯС-графа с независимой раскраской вершин и ребер сравнительно простая операция, так как в ней участвуют вершины и ребра единственного, исходного ЯС-графа, все данные которого известны. В выделяемой части TIGj с TIG составы унитарных цветов: F(G)j с F(G), F(A)j с F(A\ F{C){ с F(C) и условия существования унитарных цветов в F(G)j, F{A)i, F{C)j соответствуют условиям существования этих цветов в исходном ЯС-графе. TIGj с TIG выделяется по-разному в зависимости от условий задачи. Если в состав исходных данных входят вершины или ребра искомой части /7С-графа, то задача решается двумя путями: 1.В исходном /7С-графе задается состав А с А вершин искомого Яв-графа, а затем определяется состав С, с С ребер, инцидентные вершины которых входят в А{, и определяются унитарные цвета F(A)it F(C)j, F(G)j. Способ определения унитарных цветов зависит от условий их существования. В этом случае в TIGj могут существовать изолированные вершины. 2.В исходном ЯО-графе задается состав Су с С ребер искомого ЯС-графа, а затем определяется состав Aj с А вершин, инцидентных заданным ребрам. В этом случае в ЯС, не будут существовать изолированные вершины. К операциям выделения части ЯС-графа относится и построение путей, цепей, циклов и т.п. Выделение части Яв-графа с заданным составом вершин и ребер или дуг используется при решении задач синтеза структуры объекта из известных элементов с последующим определением функциональных свойств этого объекта, представляемых унитарной раскраской выделенной части Яв-графа. В отличие от операции выделения части Яв-графа, при вычислении разности, пересечения и объединения участвуют разные Яв-гра-фы. Если Яв-графы имеют независимую раскраску вершин и ребер, то эти операции могут выполняться раздельно над множествами вершин и ребер исходных ЯО-графов. При выполнении операций над разными ЯО-графами необходимо учитывать условия эквивалентности их вершин и ребер. Следует иметь в виду, что вычисление объединения, пересечения и разности графов TIGj и IJGj сопровождается одновременным выполнением одноименных операций над описаниями инцидентиостей Gt, Gy между вершинами и ребрами TIGj и IJGj. Если раскраски вершин и ребер в Яв-графах взаимно независимы по условиям их существования, то все виды операций над TIGj и TIGj выполняются раздельно над их множествами вершин и множествами ребер. При этом следует иметь в виду, что операция над множествами USq. , IIS с. ребер должна выполняться после операции над множествами TIS д., TISд. вершин, и в состав ребер искомого ЯО-графа включаются только те ребра, для которых имеются обе инцидентные вершины. После выполнения операций над ЯО-множест-вами вершин и ребер определяется унитарная окраска F(G) ЯО-графа. Выполнение операций пересечения и разности графов TIGj TIGj не вызывает особых трудностей, поскольку результатом их выполнения являются части исходных ЯО-графов. 2.1.5. Структурное моделирование производственных систем в CALS-технологиях Структурные модели описывают состав и взаимосвязь элементов и свойств объекта моделирования. Структурные модели играют важную роль в CALS-техпологиях как средство представления основных данных об изделиях и других объектах на всех этапах их жизненного цикла. Эти данные описываются в терминах сущностей и атрибутов на языке EXPRESS (ISO 10303-11). Математическое моделирование структуры объекта осуществляется средствами аппарата теории множеств, теории графов и математической логики. Для моделирования плохо формализуемых структур используются аппарат реляционной алгебры, семантических сетей и другие специальные средства. Весьма удобным средством структурного моделирования в CALS-техиологиях является система моделирования ИСТРА, 0 ... 39 40 41 42 43 44 45 ... 96 |












