Раздел: Документация
0 ... 28 29 30 31 32 33 34 ... 162 Точки А, В, С не лежат на одной прямой, так как векторы АВ =(1,2, -3) и АС ={2,-\, 1), параллельные прямым АВ и АС, линейно независимы (их координаты не пропорциональны). Поэтому уравнение плоскости, проходящей через точки А, В, С, согласно следствию 13.3, будет иметь следующий вид: = 0. х-\ у+3 Разложив этот определитель по последней строке, получим:
= 0, х+ 1у + 5г + 10 = 0. Это и есть уравнение искомой плоскости. Высота, опущенная из вершины D на грань ABC, должна быть перпендикулярной плоскости ЛВС, т. е. параллельна нормальному вектору этой плоскости. Так как нормальный вектор этой плоскости есть « = (1, 7, 5) (следствие 13.2), то уравнение пря- х-3 у-4 z-5 мой, проходящей через точку D параллельно вектору л , будет Глава 14Ir-zJ find Многогранники и полиэдры Условимся, что запись А + В(А - В) для двух точек А, В из Af означает точку, координаты которой равны сумме (разности) соответствующих координат точек а и В; запись ха означает точку, координаты которой получены умножением соответствующих координат точки А на число Л,, Очевидно, что между координатами точек и соединяющего их вектора существует соотношение В -А =АВ (см. гл. 12). С Определение Выпуклой комбинацией системы точек В,.....BkeAf" называется точка Л181+ ...+ХяВа, гдеХ >0, /= 1, к, U +л2+ ..».*= 1- Неотрицательной комбинацией системы V векторов из R" называется вектор, являющийся линейной комбинацией векторов системы V с неотрицательными коэффициентами. Существует несколько эквивалентных определений многогранника и многогранной области. Вот одно из них. ( Определение ) Многогранной областью, порожденной конечной системой точек Р из Af" и конечной системой векторов l/из R", называется множество всех точек изЛГ, которые представимы в виде 6 + р, где В - произвольная выпуклая комбинация точек из Р, р - произвольная неотрицательная комбинация векторов из V. Многогранником, порожденным конечной системой точек Р из Af", называется множество всех выпуклых комбинаций точек из Р. Если при этом система Рсо-стоит только из двух различных точек, то порожденный ею многогранник называется отрезком, соединяющим эти точки. На рис. 14.1 показана многогранная область в А/% порожденная точками Л, В и векторами PiiP}- Утверждение 14.1. Ограниченные многогранные области, и только они, являются многогранниками. Доказательство утверждения дано в задаче Т14.5. Напомним, что множество точек из Af" ограничено, если расстояние между любой них и нулевой точкой (0, 0,..., 0) eAfne превосходит некоторого фиксированного числа. 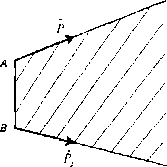 Рис. 14.1. Многогранная область С Определение ) Множество точек, содержащее вместе с любыми своими двумя точками отрезок, их соединяющий, называется выпуклым. На рис. 14.2 показано невыпуклое множество точек в Af". Утверждение 14.2. Многогранная область является выпуклым множеством.  Рис. 14.2. Невыпуклое множество точек Доказательство. Пусть G- многогранная область, порожденная точками В,fi; и векторами /*?,, р2,-.-р,„ .Докажем, что любая точка D отрезка, соединяющего Л и С, где А, С € G, принадлежит G. Согласно определениям D = \A + (\- Х)С,А=%л.1,"В, +- = ], Х{1] > О, г<п > 0, i = 1,к, j = 1,т 0 ... 28 29 30 31 32 33 34 ... 162 |












