Раздел: Документация

0 ... 6 7 8 9 10 11 12 ... 162

Е°»А =

(О0 ...0... °]

00 ...0... 0-1

00 ... 1... 0

1,0о... 0... о,

я,, я12... я,,

я„ я„

0 0

0... 0

Из равенстваЛ£/ = ЕА следует, что an = а,,-, а остальные элементы j-Vi строки и /-го столбца матрицы А равны 0. Рассматривая различные пары индексов ("и j, можно сделать вывод, что элементы главной диагонали матрицы А равны, а ее остальные элементы нулевые, т.е. А = кЕ.

Т3.5. Используем замечание3.2 и теорему 3.1: ~[Ы-у] = (хА)у-х(Ау")= = [х (Ау1)] =[х~уАт], что и требовалось доказать.

П3.21. Поскольку размеры матриц А и В равны 3*3 и 3*2, соответственно, размер

fd,, d,

матрицы равен Пусть АВ

Элемент с/] i находится на пересечении

первой строки и первого столбца, поэтому он равен скалярному произведению первой строки матрицы А на первый столбец матрицы В, т. е. du =1x1 + (-l)xl + 1х(-1) = -1; элемент rf12 равен скалярному произведению первой строки матрицы А на второй столбец матрицы так как он стоит на пересечении первой строки и второго столбца, т. е. dn ~Л х 2 + (-1) х 1 +1 х 0 = 1 . Аналогично находим:

я"г=0х1 + 1x1 + (-2) х (-1) = -1,

dn = 0x2 + 1x1 + 2x0

d„=(-l)xl + lxl + (-2)x(-l) = 2,

d3l = (-1)х2 + 1х1 + (-2)хО = -1 .

, АВ =	~ 1 1	. Умножая		все элементы матрицы АВ
	ч 2 ~])
-3 3	. Очевидно, 2С =				. Складывая элементы
6 -3

ЪАВ-

соответствующими элементами матрицы 2 С, найдем матрицу

"21 "32 aii ai

							(-3-2			?-5 Г
							-3-4			-7 -1
							6 + 2	-з + Оу		v 8 J;

Меняя строки и столбцы местами, найдем транспонированную матрицу -5 -7 81

] -1 -3

7458.0		188.8
6608.7		172.2
3551.7		160.3
4445.4		137.9
		159.5

КЗ.П. Ответы: (3060.5, 6992.6, 3188, 5121, 5567.6, 13821,485).

4 422 678.2

К3.12. Ввести исходные данные: матрицы А, В, векторы-строкиг, с. Определить годовую производительность каждого предприятия по каждому виду продукции:

ORIGIN : = 1n: = col&A) k:= 1;лC<k";=A<k> rllc

(в матрице С на позиции (к) будет число, равное годовой производительности к-го предприятия по виду продукции).

Определить годовую потребность каждого предприятия по каждому виду сырья: D: =ВТ • С (в матрице D элемент на позиции (/, к) будет равен годовой потребности предприятия в виде сырья).

Определить годовую сумму кредитования каждого предприятия для закупки сырья, необходимого для выпуска всей продукции d: = c-D (в векторе-строке d k-й элемент равен сумме, которая необходима для закупки сырья всех видов к-м

предприятием).

Глава 4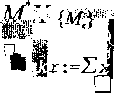

find

Метод Гаусса

Рассмотрим систему (3.1). Ее решениями являются такие наборы значений переменных Xi, ...,х„, которые превращают каждое уравнение системы в тождество. Система (3.1) однозначно определяет "расширенную" матрицу D -{АС) сп+ I столбцами, в которой матрицы А и С просто расположены рядом. В то же время любой матрице с п + 1 столбцами можно сопоставить систему линейных уравнений с п переменными: для этого достаточно считать элемент на позиции (л к) коэффициентом при переменной x/t в г-м уравнении, если к<п, и свободным членом /-го уравнения, если к = п + ]. В этих случаях матрицу и систему будем называть соответствующими. Строку расширенной матрицы будем называть противоречивой, если последний ее элемент отличен от нуля, а остальные элементы нулевые.

Утверждение 4.1. Если расширенная матрица содержит хотя бы одну противоречивую строку, то соответствующая ей система линейных уравнений не имеет ре-

Аналогично элементарным преобразованиям векторов можно рассмотреть элементарные преобразования строк матрицы:

умножение строки на любое ненулевое число (элементарное преобразование

прибавление к одной из строк другой, умноженной на любое число (элементарное преобразование типа 2).

Утверждение 4.2. Элементарные преобразования строк расширенных матриц не

изменяют множества решений соответствующей системы уравнений.

Если удалить из расширенной матрицы D последний столбец, а затем все нулевые строки (если таковые имеются), то получим так называемую приведенную матрицу D.

( Определение j

Пусть приведенная матрица D имеет размер /с х п {к<п). Если в Dсуществует к столбцов, в которых ровно по одному ненулевому элементу, причем никакие два из этих ненулевых элементов не находятся в одной строке, то переменные, соответствующие этим столбцам, называются базисными, остальные переменные - свободными. Базисные переменные составляют так называемый базис переменных.

шения.

типа 1);

0 ... 6 7 8 9 10 11 12 ... 162