Раздел: Документация
0 ... 12 13 14 15 16 17 18 ... 143 гвф эс e(t) Uer(i}u\ Двигатель aM(t) co(t) 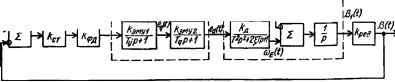 Рис. 2.4. Структурная схема следящей системы (рис. 1.14, а). точной функции видно, что сельсины как преобразователи на структурной схеме представляются пропорциональным звеном. На структурной схеме динамические звенья изображаются прямоугольниками, внутри которых записываются передаточные функции звеньев. Связи между звеньями обозначаются линиями со стрелками, указывающими направление передачи воздействий. 2.Фазовый дискриминатор описывается уравнением ифд (/) = йфДист (f), или в операционной форме £/фД (р) = £фДГ/ст (р), откуда передаточная функция фазового дискриминатора Кфд (Р) = фя(Р)/ст(Р) = *фд т. е. фазовый дискриминатор на структурной схеме также представляется пропорциональным звеном. 3.Электромашинный усилитель мощности ЭМУ состоит из двух каскадов усиления. Выходное напряжение дискриминатора поступает на обмотку управления ЭМУ (на вход первого каскада усиления). В результате воздействия этого напряжения в поперечной цепи ЭМУ индуктируется э. д. с. eq (t). Найдем уравнение, связывающее между собой eq (f) и ИфД (f). Уравнение напряжения в обмотке управления ЭМУ (2.26) %b«) = Ryiy (t) + Lydi(t)/dt, где Ry и Ly — активное сопротивление и индуктивность цепи обмотки управления ЭМУ. Электродвижущая сила, индуктируемая в поперечной цепи ЭМУ: eq (t) = c,iy (t).(2.27) Подставив в (2.26) значение iy (г) = eq (f)/c1 из (2.27) и разделив (2.26) на Ry, получим "ФдЮ МО /.у deq (t) dt RyCj ftyCj Умножив левую и правую части полученного уравнения на Cj и записав его в принятой в автоматике форме, будем иметь Tydeq (t)ldt + eQ (t) = £ЭЛ1У1ифд (0,(2.28) где Ту = LylRy — постоянная времени цепи обмотки управления ЭМУ; кэму1 =» = Cj//?y — коэффициент усиления первого каскада ЭМУ. Запишем уравнение (2.28) в операционной форме: (Тур + 1) Eq (р) = кЭМУ1 l/фд (р), откуда передаточная функция первого каскада ЭМУ «ЭМУ! (Р) = Eq (р)/1/фд (р) = кЭМУ11(Тур + 1),(2.29) т. е. первый каскад ЭМУ на структурной схеме представляется апериодическим звеном. Найдем уравнение и передаточную функцию второго каскада ЭМУ, входом которого является поперечная, а выходом — продольная цепь ЭМУ. Входной величиной каскада является э. д. с. eq (f), а выходной — э. д. с. (г), индуктируемая в продоль- ной иепи. Уравнение напряжения в поперечной цепи ЭМУ: е„ (О = 1„ (О Я, + V« W/*.(2- 3°) где Rq и Lg — активное сопротивление и индуктивность поперечной цепи ЭМУ. Электродвижущая сила, индуктируемая в продольной цепи ЭМУ, ed(t)=q(i).(2.31) Исключив из формул (2.30) и (2.31) промежуточную переменную iq (г), получим Tqded (0/Л + ed (0 = k3My2eq (t),(2.32) Где Tq = Lq/Rq — постоянная времени поперечной цепи ЭМУ; кЭМУ2 = c2/Rq — коэффициент усиления второго каскада ЭМУ. В операционном виде уравнение (2.32) имеет вид (Tqp + 1) Ed (р) = k3My2Eq (р), откуда передаточная функция звена Кэмуч (Р) = £d (P)/£e (Р) = ЬЭШ21(Т„р + 1), т. е. второй каскад ЭМУ на структурной схеме также представляется апериодическим звеном. 4. Выход ЭМУ в следящей системе включен на двигатель постоянного тока с независимым возбуждением. Рассмотрим участок системы, включающий продольную цепь ЭМУ — двигатель. Входнойвеличиной этого участка является э. д. с. ed (f), индуктируемая в продольной цепи ЭМУ, а выходной — частота вращения и (0 двигателя. Найдем уравнение, связывающее и (0 и ed (0- Уравнение для э. д. с. ed (0 в электрической цепи, состоящей из продольной цепи ЭМУ и обмотки якоря двигателя, имеет вид Ъ (0 = RJd W + Lddid (0/Л + едв (0,(2.33) где Rd = (Яя + Як.0 + Кд.п + Яидэму + (*я + * д.п + #щ)дв; = (Гя + LKO + £.д.п)ЭЛ1у + (L„ + д.п)дв, Яя. Ядп, /?к-0. Ящ — активные сопротивления обмоток якоря, дополнительных полюсов, компенсационной обмотки, щеток соответственно; Ья, £дп, LKO — индуктив-. ности обмоток якоря, дополнительных полюсов и компенсационной обмотки; едв (0 = ссо (0 Ф — противо-э. д. с. Поскольку рассматривается двигатель с независимым возбуждением, то, пренебрегая влиянием потока реакции якоря, можно считать, что магнитный поток двигателя Ф = const и тогда едв(0 = М>(0. ке = сФ. Подставив значение едв (0 в уравнение (2.33), получим ей (0 = Ruh (0 + Ladid (О/Л + keu (t).(2.34) Выражение (2.34) представляет собой только уравнение для э. д. с. в рассматриваемой цепи. Однако в этой цепи есть и механическая энергия, поэтому необходимо составить уравнение моментов. Образуемый в двигателе момент вращения Мвр уравновешивается моментом сопротивления Мс и динамическим моментом Jde> (f)Idt, т. е. м*р = мс + Jda) (0/Л, где J — + (1/<?2) Jpu — момент инерции всех вращающихся частей, приведенных к валу двигателя, Н • м • с2; Уда, Jp м — моменты инерции двигателя и рабочего механизма соответственно; q — передаточное число редуктора; Мс = Мсры/д — момент сопротивления рабочего механизма, приведенный к валу двигателя, Н • м; М0 р м — момент сопротивления рабочего механизма. Момент вращения двигателя Мвр = kft>id (f), или, учитывая, что Ф = const, AIBp = Vd(0. км = кФ. Подставив значение Мвр в уравнение моментов, получим (0 = Мс + Jda (t)/dt. Из последнего уравнения находим id(f) = Mc/kM + (J/ku)d<i>(t)/dt и подставляем в уравнение (2.34): Разделив это уравнение на ke, получим . Ld JRd Jtoffl JRd dm(t)ed(t) Rd Rd kMke dP + kKke dt t-aV>- kekMke /W° или ТэТы(Ры (О/Л2 + TKdm {t)ldt + со (t) = V«f W - kmMc, где Tg = Ld/Rd — электромагнитная постоянная времени цепи, с; Т„ — JRd/kKke — электромеханическая постоянная времени, с; kR=l/ke — коэффициент усиления двигателя по отношению к ed (t); £дм = Riilkuke —■ коэффициент усиления двигателя по отношению к Мс. Обозначим ТЭТЫ = Т2, Ты= 26Т; тогда последнее уравнение примет вид TWa (t)ldt* + 2lTdw (t)ldt + со (г) = (0 - *Л или в операционной форме (7>2 + 2£7> +1)со (р) = kAE4 (р) - kmMc (р), откуда находим ю(р) = щ(р) — шк (р), где Ше W = TV + 2+1 £d W Шм (р) = 7уА>+1 М° (Р) изображения составляющих частоты вращения двигателя, вызванных — э. д. с. ed (t) на входе участка и моментом сопротивления Мс (t) соответственно. Как видно из последней формулы, частота вращения двигателя со (f) зависит от ed (0 и Мс (f). Из выражения для сог (р) находим передаточную функцию участка (двигателя), связывающую сое (f) и ed (f), *«(Р) = ~ЕШ = T>p*+k2ZTP+l •(2-35) а из формулы для (р) — передаточную функцию, связывающую % (Q и Мс (f), Им(Р) = feAM(2 Ш *amW- Л1с(р)Г2р2 + 27> + 1 где g = тЫ/2Т = (1/2) Ytu/T3 — относительный коэффициент затухания. Полученные передаточные функции соответствуют передаточной функции колебательного звена (2.16). Поэтому участок, включающий продольную цепь ЭМУ — двигатель, на структурной схеме (рис. 2.4) представляется двумя каналами, в каждом из которых содержится соответствующее колебательное звено; выходные сигналы звеньев вычитаются. Как указывалось, характер колебательного звена зависит от относительного коэффициента затухания . Если > 1, то в соответствии с формулой (2.21) каждое колебательное звено заменяется двумя апериодическими; а при 1 — одним апериодическим звеном. Как видно из выражения для , значение > 1 возможно, если Ты > 47,э, что практически всегда выполняется. 0 ... 12 13 14 15 16 17 18 ... 143 |












