Раздел: Документация
0 ... 24 25 26 27 28 29 30 ... 143 Для получения ЛАЧХ звена L (со) в области высоких частот необходимо сложить прямые 20 lg k и —20 lg со Т. Такое сложение показано на рис. 2.20. Как видно из рисунка, ЛАЧХ апериодического звена в области высоких частот представляет прямую СВ с наклоном —20 дБ/дек. Таким образом, ЛАЧХ апериодического звена представляется горизонтальным (А С) и наклонным с S = —20 дБ/дек (СВ) отрезками прямых, являющимися асимптотами точной ЛАЧХ в области низких и высоких частот. Найдем частоту щ, соответствующую точке С сопряжения гори-аонтальной и наклонной асимптот. Поскольку точка С принадлежит обеим прямым, то на частоте а>х правые части выражений (2.103) и (2.104) будут равны между собой: 20 lg к — 20 lg k — 20 lg сохТ. Из последнего выражения следует: 201gco17 =0, или cojT = 1, откуда а>х = 1/Т, т. е. значение частоты, при которой происходит сопряжение низко-1 и высокочастотной асимптот, равно 1/Т. Эта частота называется частотой сопряжения. Можно рекомендовать следующий порядок построения ЛАЧХ апериодического звена: 1) вычислить 20 lg k и полученное значение отложить по оси ординат (точка А, рис. 2.20); 2) вычислить частоту сопряжения а>х = 1/Т, отложить ее значение на оси частот; 3) на уровне 20 lg k провести горизонтальный отрезок от оси ординат до частоты сопряжения сох (отрезок АС); 4) из точки сопряжения С провести отрезок прямой под наклоном —20 дБ/дек (отрезок СВ). Ломаная линия АСВ представляет собой ЛАЧХ апериодического звена. Точная ЛАЧХ звена показана на рис. 2.20 кривой Lj (со). Как видно из рисунка, она совпадает с приближенной асимптотической ЛАЧХ L (со) при со cox и со > сох. Наибольшая погрешность при замене точной ЛАЧХ ее асимптотами имеет место при частоте сопряжения сох = 1/Т и равна 3 дБ. Форма ЛАЧХ звена не зависит от его коэффициента усиления k. Изменение k приводит лишь к параллельному перемещению характеристики. Если k — 1, то горизонтальный отрезок ЛАЧХ будет совпадать с осью 0 дБ. Для случая k — 1 ЛАЧХ звена на рис. 2.20 изображена ломаной mnl. Выражение для ЛФЧХ апериодического звена: i) (со) = —arctg со Т. Для построения ЛФЧХ звена необходимо задаться различными частотами со и определить значения ординат характеристики на этих частотах. Для выяснения вида ЛФЧХ звена достаточно определить яр (со) для следующих трех частот:
ЛФЧХ апериодического звена изображена кривой ф (со) на рис. 2.2Q. Обратим внимание на то, что ЛФЧХ звена при частоте сопряжения сох = 1/Т имеет ординату, равную —45°. Из сравнения ЛАЧХ и ЛФЧХ видно, что в области частот, где ЛАЧХ представляет горизонтальную прямую, ЛФЧХ стремится,к 0°, а там, где ЛАЧХ выражена прямой с наклоном —20 дБ/дек, ЛФЧХ стремится к —90°. Резкие изменения ЛФЧХ имеет только около частоты сопряжения, где ЛАЧХ изменяет наклон. Логарифмические частотные характеристики колебательного звена. КПФ устойчивого колебательного звена: К (/со) = Щ\ — Т2со2 + /2Тсо) = N (со) еть>),(2.105) где N (со) =k; гр (со) = — arctg 2T(i> . Выражение для ЛАЧХ звена: L (со) = 20 lg N (со) = 20 lg k — 20 lg V(l — T2co2)2 + (2Тсо)2. Если принять & = 1, то L (со) = — 20 lg ]/(1 TW)2 + (2Тсо)2.(2.106) Для области низких частот, где со < 1/Т и поэтому можно пренебречь членами Т2 и (2Тсо)2 по сравнению с единицей, последнее выражение можно написать в приближенном виде: L (со) = —201gj/l = 0, т. е. в области низких частот ЛАЧХ колебательного звена при k== 1 будет совпадать с осью 0 дБ (рис. 2.21, а). В области высоких частот, а именно при 1/Т, когда 1 <Т2со2 и (2Тсо)2 < (Т2со2)2, можно написать следующее приближенное равенство: К(1 — Т2со2)2 + (2£Тсо)2 » Т2со2, а выражение (2.106) для ЛАЧХ примет вид: L (со) = — 20 lg (Тсо)2 = — 2 • 20 lg Тсо = — 40 lg Тсо. При построении ЛАЧХ апериодического звена было показано, что график, изображающий —20 lg Тсо, является прямой с наклоном —20 дБ/дек. Очевидно, что L (со) == —2 • 20 lg Тсо будет изображаться прямой с наклоном, равным —40 дБ/дек (рис. 2.21, а). Таким образом, приближенная асимптотическая ЛАЧХ колебательного звена изображается двумя отрезками прямых: горизонтальным отрезком, при k = 1, совпадающим с осью 0 дБ, и отрезком с наклоном — 40 дБ/дек. Горизонтальный отрезок является асимптотой точной ЛАЧХ в области низких, а наклонный — в области высоких частот. Низкочастотная и высокочастотная асимптоты ЛАЧХ сопрягаются при частоте сопряжения к»!, определяемой из уравнения —20 lg 1 = = —40 lg щТ, т. е. при частоте щ = 1/Т. Можно рекомендовать следующий порядок построения асимптотической ЛАЧХ колебательного звена для случая Ь,ф\\ 1) на уровне 20 lg k провести горизонтальный отрезок (отрезок АВ) до частоты сопряжения щ = 1/Т; 2) из точки сопряжения В провести отрезок прямой под наклоном —40 дБ/дек (отрезок ВДЕ). Для этого от частоты сопряжения (точка В) отложить вправо одну декаду и от новой точки (точки С) отложить вниз 40 дБ. Затем провести отрезок прямой через точки В и Д...... L(a),dS ф),дБ <I0  20lgk 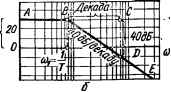 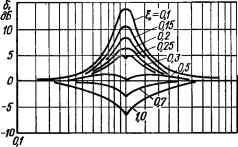 Рис. 2.21. Асимптотическая логарифмическая амплитудно-частотная характеристика колебательного звена: а — k= \; б — ft > 1. Ломаная прямая АВДЕ будет представлять ЛАЧХ колебательного звена. Точные ЛАЧХ колебательного звена отличаются от асимптотической ЛАЧХ. Эти отклонения в сильной степени зависят от коэффициента относительного затухания входящего в выражение передаточной функции. Добавляя поправки б (рис. 2.22), соответствующие различным значениям g, к асимптотической ЛАЧХ, мож-яю получать точные ЛАЧХ (рис. 2.23, а). Из рис. 2.22 видно, что при значениях, лежащих в пределах 0,38 £ < 0,7, отклонения не превосходят 3 дБ и поэтому, как и при построении ЛАЧХ апериодического звена, могут не учитываться. Выражение для ЛФЧХ колебательного звена:- ф (to) = arctg [2£Тсо/( 1 — Ггсо2)]. / Логарифмические фазо-частотные характеристики при различных значениях приведены на рис. 2.23, б, из которого видно, что ЛФЧХ звена изменяются от 0° в области низких частот до —180° в области высоких частот. На частоте сопряжения сох = l/Т сдвиг по фазе равен —90°. 0,2 0,30fi0,5 0,810 2 3 4 5678910 6)/U)f Рис. 2.22. Поправки к ЛАЧХ колебательного звена, соответствующие различным -значениям . Логарифмические частотные характеристики систем автоматического управления в разомкнутом состоянии Методику построения ЛАЧХ систем автоматического управления рассмотрим на примере системы, состоящей из последовательно соединенных двух апериодических и одного интегрирующего звеньев, комплексная передаточная функция которой имеет вид: Яр О) = VI/» № + (ТУсо + 1)1 = N (ш) е*(ю). 0 ... 24 25 26 27 28 29 30 ... 143 |












