Раздел: Документация
0 ... 25 26 27 28 29 30 31 ... 143 ID 0 -10 -20 -30 OJ 0,2 Q3 Q4Q5Q6Q8iO 2 3 4 5 68шГ a 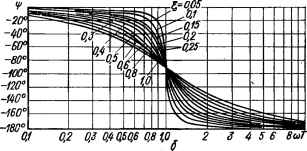 Рис. 2.23. Точные логарифмические амплитудно-частотные и фазо-частотные характеристики колебательного звена при различных значениях £: а — ЛАЧХ; б — ЛФЧХ. Учитывая, что модуль произведения комплексных чисел равен произведению модулей этих чисел, а аргумент произведения равен сумме аргументов сомножителей, можем записать: Л» = у(со11/7V+ 1);io7) ■ф (со) = — к/2 — arctg со7\ — arctg соТ2. Выражение для ЛАЧХ системы: L (со) = 20 lg N (со) = 20 lg ftp — 20 lg со — 20 lg ]/ Г2со2 + 1 - — 20 lg /7V+~1,(2.108) т. е. ЛАЧХ системы равна сумме ЛАЧХ последовательно включенных звеньев. Для построения ЛАЧХ системы построим сначала ЛАЧХ звеньев, соответствующих слагаемым выражения (2.108), а затем сложим ординаты ЛАЧХ всех звеньев. Указанные построения выполнены на Рис. 2.24. Первое слагаемое выражения (2.108) Ьг (со) = 20lg/jp графически изображается, прямой Ьг (со), проведенной параллельно оси абсцисс  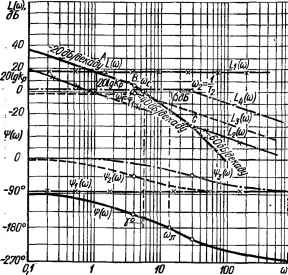 Рис. 2.24. Пример построения логарифмических частотных характеристик системы в разомкнутом состоянии. на уровне 20 Ig kp. Второе слагаемое L2 (со) = —-20 lg со, представляющее собой выражение для ЛАЧХ интегрирующего звена, как было показано, на графике изображается прямой L2 (со) с наклоном — —20 дБ/дек, пересекающей ось 0 дБ при частоте со = 1. Третье и четвертое слагаемые L3 (со) = —20 lg Vсо2 + 1, L4 (со) = —20 lg VTfco2 + 1 представляют собой выражения для ЛАЧХ апериодических звеньев в случае, если их коэффициенты усиления равны единице. Графически изображаются горизонтальными отрезками и отрезками с наклоном —20 дБ/дек, сопрягающимися при частотах сопряжения, соответственно равными со2 == l/Tt и со2 = 1/Т2. ЛАЧХ системы, полученная сложением ординат ЛАЧХ отдельных звеньев, на рис. 2.24 изображена ломаной L (со). При построении ЛАЧХ системы обычно не строят ЛАЧХ отдельных звеньев, а придерживаются следующей методики: 1) определяют сопрягающие частоты colt со2, со„ (для рассматриваемого примера =1/7,, со2 =\1Т2) и откладывают вдоль оси частот (рис. 2.24); 2) на частоте со = 1 откладывают ординату, равную 20 lg kp, где kp — коэффициент усиления разомкнутой системы (точка А); 3) через точку А проводят прямую с наклоном — v 20дБ/дек (где v — порядок аста-тизма системы, для нашего случая v — 1) до первой частоты сопряжения с»! (точка В). Этот отрезок будет низкочастотной асимптотой ЛАЧХ системы. Если окажется, что первая частота сопряжения со,<;1. то через точку А пройдет продолжение низкочастотной асимптоты; 4) после каждой из частот сопряжения со необходимо изменять наклон ЛАЧХ на —20 дБ/дек, если частота сопряжения определяется постоян- 1ше 20lgkp U- 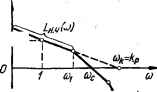 Рис. 2.25. К определению частоты cofc. ной времени сомножителя (Т{/ю +1) знаменателя передаточной функции, и на +20 дБ/дек, если эта частота определяется постоянной времени сомножителя числителя. В рассматриваемом примере все сомножители находятся в знаменателе КПФ, поэтому при eoj и со2 необходимо изменять наклон ЛАЧХ на —20 дБ/дек. При наличии колебательных звеньев наклон ЛАЧХ изменяют на ±40 дБ/дек. Найдем частоту щ, при которой низкочастотная асимптота ЛАЧХ системы или ее продолжение пересекает ось 0 дБ (рис. 2.25). Если система имеет астатизм 1-го порядка (v = 1), то низкочастотная асимптота и ее продолжение определяются суммой первых двух членов выражения (2.108): Z-н.ч (со) = 20 \gkp— 201gco. В точке пересечения асимптоты или ее продолжения с осью 0 дБ имеем LH.4 (coft) = 20 lg kv — — 20,lg щ = 0, откуда искомая частота coft = kp. Это свойство можно использовать при построении низкочастотной асимптоты ЛАЧХ: на оси 0 дБ следует отметить точку, соответствующую частоте щ = kp, и через эту точку провести (пунктирную) прямую с наклоном —20дБ/дек. Низкочастотная ЛАЧХ системы будет совпадать с этой прямой до первой частоты сопряжения cot. Дальнейшее построение ЛАЧХ выполняется в соответствии с п. 4 изложенной выше методики. Используя свойство щ = kp, можно непосредственно по ЛАЧХ определить коэффициент усиления системы kp. Для этого достаточно определить частоту cofe в точке пересечения низкочастотной асимптоты ЛАЧХ или ее продолжения с осью 0 дБ. Если система имеет астатизм второго порядка (у = 2), то уравнение пересечения низкочастотной ЛАЧХ (или продолжения асимптоты) с осью 0 дБ имеет вид: LH.4 (щ) = 20 lg — 20 lg со = 0, откуда cofe =\fkp. Для построения низкочастотной асимптоты ЛАЧХ в этом случае необходимо через точку на оси 0 дБ, соответствующую частоте сод = V~kp, провести прямую с наклоном —40 дБ/дек. Частота сос, при которой модуль КПФ системы N (сос) = 1, называется частотой среза. Учитывая, что L (сос) = 201g/V (сос) =0, частотой среза сос будет, частота, при которой ЛАЧХ пересекает ось 0 дБ (рис. 2.25). Выражение для ЛФЧХ системы: ф (со) = — к/2 — arctg щТх — arctg соТ, т. е. ЛФЧХ системы может быть получена так же, как и ЛАЧХ системы: простым сложением ординат ЛФЧХ звеньев, входящих в систему. Однако на практике вычисляют значения ЛФЧХ системы аналитически. Для этого удобно составить таблицу следующей формы:
0 ... 25 26 27 28 29 30 31 ... 143 |












