Раздел: Документация
0 ... 22 23 24 25 26 27 28 ... 143
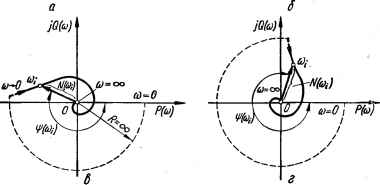 Рис. 2.15. АФЧХ статической и астатических систем: с — статической системы; б — г — астатических систем, имеющих астатизм 1—3-го порядка соответственно. АФЧХ системы с астатизмом 1-го порядка в разомкнутом состоянии. Пусть КПФ системы определяется выражением тп—I Кр (/со) = k р П (1 + /соТ;-)//со П (1 + /соТ,) = N (со) ет<*\ п>т. При to -> О сомножители числителя и знаменателя, взятые в скобки,, стремятся к елинице, вследствие чего КПФ системы при со -+0 прибли-. жается к КПФ интегрирующего звена, т. е. Kp(ja) = kv/jco = {kp/(i>)e-/Il/2 = N(co)ema\ где N (со) = fep/co; ij) (со) = —л/2, следовательно, при со -*■ оо : N (со) -*• оо; \\> (со) -*--я/2. Примерный вид АФЧХ системы с астатизмом 1-го порядка показан на рис. 2.15, б. Как видно из рисунка, при со ->• 0 амплитуда выходных колебаний в этих системах стремится к бесконечности, а сдвиг по фазе к —я/2. Такой вид АФЧХ системы с астатизмом первого порядка при со ->• О объясняется тем, что при со ->• 0 свойства всей системы, как было показано, определяются свойствами интегрирующего звена. Бесконечно большое значение N (со) при со О с физической точки зрения можно объяснить следующим образом. При со =0 на вход разомкнутой системы подается постоянный по значению сигнал е0. Поскольку система содержит интегрирующее звено (например, двигатель), его выходная величина (угол поворота якоря двигателя) при этом будет безгранично возрастать. Поэтому N (со) = р7б0 будет увеличиваться до бесконечности. При со = 0 понятие о сдвиге по фазе между входной и выходной величинами теряет смысл. В этом случае можно считать, что АФЧХ астатической системы (интегрирующего звена) начинается в бесконечно удаленной точке, расположенной на положительной вещественной оси, но уже на самых малых частотах идет по дуге бесконечно большого радиуса, показанной на рис. 2.15, б пунктиром. При частоте со = со /V (со) =0, гр (со) =—(п — т) 90°. Если, например, п — т = 4, то Ф (со) = —360 °, т. е. АФЧХ системы проходит по часовой стрелке четыре квадранта (рис. 2.15, б). АФЧХ систем с астатизмом 2-го и 3-го порядка изображены соответственно на рис. 2.15, в, г. 2.8. Логарифмические частотные характеристики звеньев и систем автоматического управления Определение логарифмических частотных характеристик Построение амплитудно-фазовых частотных характеристик сложных систем связано с большой затратой времени. Исследование САУ значительно упрощается, если пользоваться частотными характеристиками, вычерченными в логарифмическом масштабе, т. е. логарифмическими частотными характеристиками (ЛЧХ). Простота метода ЛЧХ объясняется простотой построения характеристик: логарифмическая частотная характеристшга системы получается сложением характеристик отдельных звеньев [при построении АФЧХ системы необходимо перемножать АФгл отдельных ее звеньев); точные логарифмические характеристики..звеньев заменяются отрезками прямых — асимптотами. Выясним, что представляют собой ЛЧХ. Запишем комплексную передаточную функцию в показательной форме К (/**) = N (&) eW«") и прологарифмируем выражение для К (/ю): In К (/со) = In [N (со) е***] = In N (со) + /ф (со). Кривая зависимости логарифма модуля In N (со) комплексной передаточной функции от частоты, отложенной по оси абсцисс в логарифмическом масштабе, называется логарифмической амплитудно-частотной характеристикой (ЛАЧХ). Обычно на графике по оси ординат принято откладывать не In N (со), а пропорциональную ей величину L (со) = 20 lg N (со) [lg N (со) = 0,434 In N (со)], измеряемую в децибелах. При сравнении двух величин с7т2 и 1/тг говорят, что они отличаются на 1 дБ, если 20lg (Um2/Uml) = 1. Зависимость аргумента г]э (со) КПФ от частоты, отложенной по оси абсцисс в логарифмическом масштабе, называется логарифмической фазо-частотной характеристикой (ЛФЧХ). Ig0,1=-1IghO lg2=OJ01 fgfO=flg100=2 i i ......... i to0 0,11 2 3 4 5678310,„„ *>
Рис. 2.16. Логарифмический масштаб частоты. При построении логарифмического масштаба частоты по оси абсцисс откладываются отрезки, пропорциональные не самим частотам со, а логарифмам частот lgco, как показано на рис. 2.16. Для удобства пользования логарифмическим масштабом частот на оси абсцисс обычно наносятся значения самих частот, логарифмы которых отложены по оси. Рассмотрим понятия об октаве и декаде. Если две частоты сох и со2 отличаются друг от друга в два раза, т. е. coa/coj = 2, то говорят, чТо эти частоты отличаются друг от друга на одну октаву. Если же частоты со, и со2 отличаются друг от друга в 10 раз, т. е. ы2/®1 = 10, то считают, что эти частоты отличаются на одну декаду. Декада — интервал между частотами, отличающимися друг от друга в 10 раз. Например, интервал частот от щ =0,1 до со2 = 100 содержит 3 декады: 1-я декада — между со, = 0,1 и со =1, 2-я декада — между со = 1 и со = = 10 и 3-я декада — между со = 10 и со2 = 100. Отрезок, изображающий декаду (или октаву) в логарифмическом масштабе, имеет одну и ту же длину для любого участка оси частот, равную lg (10со/со) = = lg 10 = 1 (см. рис. 2.16). Рассмотрим логарифмические амплитудно- и фазо-частотные характеристики динамических звеньев. Логарифмические частотные характеристики динамических звеньев Логарифмические частотные характеристики пропорционального звена. Комплексная передаточная функция звена К (/со) = k = N (со) еша), где N (со) = k; ф (со) = 0. Выражение для ЛАЧХ L (со) = 20 lg N (со) = 20 lg k, т. е. ЛАЧХ звена не зависит от частоты и поэтому представляет прямую, параллельную оси частот (рис. 2.17). Если k>\, то ЛАЧХ проходит выше оси абсцисс, при k < 1 — ниже оси. Выражение для ЛФЧХ: г]э (со) = 0, т. е. логарифмическая фазо-частотная характеристика не зависит от частоты и представляет прямую, совпадающую с положительной вещественной осью (прямая ф (со), рис. 2.17). Логарифмические частотные характеристики интегрирующего звена. Комплексная передаточная функция звена: К (/со) = k/ja = (Л/со) е /я/2 = N (со) em<a\ где N (со) = ft/со; я> (со) = —я/2. 78 0 ... 22 23 24 25 26 27 28 ... 143 |
|||||||||||||||||||||||||||












