Раздел: Документация
0 ... 20 21 22 23 24 25 26 ... 143 т. е. аргумент ф (to) КПФ равен сдвигу фаз между выходным и выходным колебаниями. Из формулы (2.92) видно, что ■ф (со) есть функция частоты со. Кривая зависимости аргумента г]з (со) КПФ от частоты называется фазочастотной характеристикой (ФЧХ). ФЧХ апериодического звена определяется формулой (2.92). Амплитудно-фазовая частотная характеристика (АФЧХ) г ( Комплексную передаточную функцию К (/со) при со,- можно изобразить вектором в полярной системе координат (рис. 2.11, а). Длина этого вектора определяется модулем N (со,), а угол его поворота относительно полярной оси — аргументом 1}> (со,) КПФ. Обычно полярную систему координат совмещают с декартовой (рис. 2.11, б). За полюс принимается начало декартовых координат, а за полярную ось — положительная вещественная ось. Поскольку N (со) и яр (со) являются функциями частоты, длина вектора N (со) и угол его поворота изменяются с изменением со (рис. 2.11, в). Кривая, описываемая концом вектора комплексной передаточной функции К (/со) звена (системы) при изменении частоты со от 0 до оо (годограф вектора К (/со), называется амплитудно-фазовой частотной характеристикой звена (системы). Амплитудно-фазовую частотную характеристику апериодического звена можно построить в декартовой и полярной системах координат. 1. Для построения АФЧХ в декартовой системе координат КПФ звена представляют в алгебраической форме: К (/со) = А/(Г+ /соГ) = Р (со) + jQ (со), где Pico) = k/(l + со2Г2); Q (со) = — kTw/(l + co2) — (2.95) выражения для вещественной и мнимой частотных характеристик звена соответственно. Задаваясь различными значениями частоты со(, определяют соответствующие значения Р (со) и Q (со), которые являются координатами точек АФЧХ в декартовой системе координат. Уравнения (2.95) представляют собой параметрические уравнения АФЧХ апериодического звена с параметром со. Исключение этого параметра 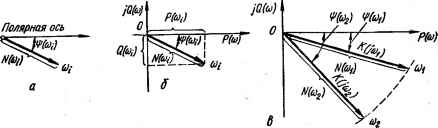 Рис. 2.11. Изображение вектора комплексной передаточной функции К (/со): о — в полярной системе координат; б — в декартовой системе координат; е — изменение вектора К (усо) с изменением частоты «а. 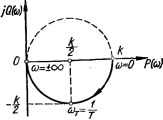 Рис. 2.12. АФЧХ ского звена. апериодиче- дает уравнение АФЧХ в декартовых координатах Р (со) и Q (со) в виде [Р (и) /г/2]2 + £2 (со) = (А/2)2- Это уравнение окружности, касающейся мнимой оси в начале координат, с центром на вещественной оси в точке (ft/2, 0), диаметром k (рис. 2.12). Нижняя полуокружность АФЧХ соответствует частотам со от 0 до +оо, а верхняя — от 0 до —со. Физический смысл имеют только частоты от 0 до +оо, поэтому обычно изображают ту часть АФЧХ, которая соответствует изменению от 0 до + со. Для определения характерных точек АФЧХ апериодического звена зададимся некоторыми частотами и вычислим по формулам (2.95) значения Р (со) и Q (со). В соответствии с полученными данными (тФ • 2.2) на АФЧХ отмечаем частоты. 1 ,ели АФЧХ снята экспериментально, то из нее можно определить параметры k и Т звена. Коэффициент k определяется непосредственно из АФЧХ, как длина отрезка на вещественной оси от начала координат до точки АФЧХ, соответствующей со =0. Чтобы определить Т, находится частота со7, соответствующая точке АФЧХ, где Q (и>т) = = Ы2, затем Т находится как величина, обратная сог, т. е. Т = 1/сог. 2. Для построения АФЧХ в полярной системе координат КПФ представляют в показательной форме: К (/со) = г = е-"arc(g aT = N (со) е*™ и У со2Г2 +1 где N (со) = fe/]/co2T2 + 1 — модуль КПФ; г) (со) = — arctg соТ — аргумент КПФ. Задаваясь различными значениями частоты со, определяют N (со) и (со) (табл. 2.3) и откладывают их в полярной системе координат, совмещенной с декартовой (рис. 2.13, а). Из выражений для N (со), (со) и АФЧХ апериодического звена видно, что с увеличением частоты со модуль N (со) уменьшается, а аргумент г]) (со) по абсолютному значению увеличивается. Это согласуется с физическими представлениями о процессах в электрической Таблица 2.2. Значения функций Р(со) и <? (со) Таблица 2.3 Значения функций N (со) и ф (ш)
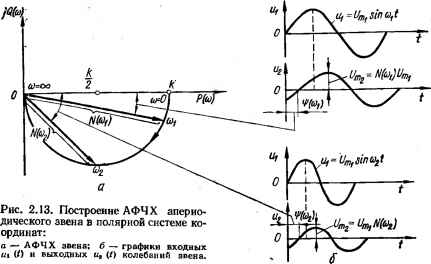 цепи (рис. 2.2, а). При подаче на вход цепи постоянного напряжения (со = 0) выходное напряжение после окончания переходного процесса ы2 (t) = kux (/), k == R2 /(Rx + R2), откуда k = u2 (f)lux (f). Постоянное напряжение можно считать частным случаем переменного напряжения, когда со = 0, а амплитуда равна значению постоянного напряжения (их (t) = Umi, и2 (f) = Um2). Поэтому можно написать k = и2 (t)lux (0 = Una/Umi = N (соо- Понятие о фазовом сдвиге при со = 0 теряет свой смысл. В этом случае (со)а==0 = 0. При подаче на вход схемы синусоидального напряжения их (t) = = Umi sinco/ ток в цепи из-за индуктивности L отстает по фазе от входного напряжения их if). Следовательно, будет отставать по фазе от их (0 и напряжение ы2 (г) на выходе схемы, так как и2 (i) снимается с активного сопротивления Ri и совпадает с током по фазе. Из-за падения части подводимого напряжения на индуктивном сопротивлении xL = coL напряжение и2 (t) по сравнению со случаем со = 0 уменьшается. Следовательно, уменьшается и модуль N (со). С увеличением частоты со из-за влияния L угол отставания Ф = г]э (со) увеличивается, а амплитуда выходных колебаний Um2 при условии, что Umi = const, уменьшается. Из последнего следует, что с увеличением to модуль N (to) = ИтчЮтх уменьшается. • На рис. 2.13, б изображены графики колебаний напряжения на входе их (t) и выходе «2 (г) цепи для частот щ и со2 (to2 > tOx). На этом же рисунке иллюстрируется связь между АФЧХ цепи и параметрами колебаний на ее входе и выходе. 0 ... 20 21 22 23 24 25 26 ... 143 |












