Раздел: Документация
0 ... 21 22 23 24 25 26 27 ... 143 Амплитудно-фазовые частотные характеристики динамических звеньев Амплитудно-фазовая частотная характеристика пропорционального звена. АФЧХ звеньев и системы строятся на основании выражений для комплексных передаточных функций. Последние, как отмечалось, можно определять из передаточных функций, заменяя р на /со. Передаточная функция пропорционального звена К (р) = k, следовательно, КПФ этого звена /С (/со) = А. При построении АФЧХ в полярной системе координат представляем КПФ в показательной форме: К (/со) = N (со) е/*(а),(2.97) где N (со) = k, $ (со) =0. Из формулы (2.97) и АФЧХ (рис. 2. К, а) видно, что модуль N (со) (а следовательно, и амплитуда выходных колебаний) не зависит от частоты, а также, что г]э (со) = ср = 0, т. е. выходные колебания совпадают по фазе с колебаниями на входе на всех частотах. Амплитудно-фазовая частотная характеристика интегрирующего звена. Передаточная функция интегрирующего звена К (р) — k lpt откуда, заменяя р на /со, получаем КПФ звена: /С(/со) = Л//со = —/fe/co.(2.98) Учитывая, что — / = е~/"я/2, последнее выражение можем написать в виде К (/со) = (А/со) е /я/2 = N (со) ета\(2.99) где N (со) = А/со; г]э со) = — я/2. Из формулы (2.99) и АФЧХ (рис. 2.14, б), построенной в соответствии с этой формулой, видно, что при со = 0 N (со) = со, с увеличением со (на АФЧХ направление увеличения со будем обозначать стрелкой) N (со) уменьшается и при со = со N (со) = 0. Аргумент г]э (со) не зависит от частоты и равен — я/2, т. е. интегрирующее звено вносит запаздывание колебаний по фазе, равное 90°, на всех частотах. Амплитудно-фазовая частотная характеристика идеального дифференцирующего звена. Передаточная функция звена К (р) = tp, № 0 K(jo) РМ я= ■со С7 Ъ>) а*0 jQ&o) й) со 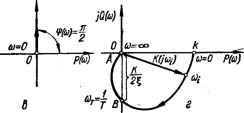 Рис. 2.14. АФЧХ динамических звеньев: о — пропорционального; 6 — интегрирующего; в — идеального Дифференцирующего; г — колебательного. Таблица 2.4. Значения функций N (со) и ф (со)
/сот = соте/я/2 - откуда КПФ звена: К (/со) = Л(со)е/*<ш)>(2.100) где N (со) = сот; -ф (со) = я/2 — модуль и аргумент КПФ. Из формулы (2.100) и АФЧХ (рис. 2.14, в), построенной в соответствии с этой формулой, видно, что при со = 0 /V (со) = 0, с увеличением со N (со) увеличивается и при со = со N (со) = оо. Аргумент i) (со) не зависит от частоты и равен я/2, т. е. идеальное дифференцирующее звено вносит не запаздывание колебаний по фазе, как другие звенья, а опережение. Это опережение равно я/2 на всех частотах. Амплитудно-фазовая частотная характеристика колебательного звена. Передаточная функция колебательного звена k (р) = k/(T2p2 + + 2\Тр + 1), откуда его КПФ: К (/со) = Щ1 — Г2со2 + /2Гсо) = N (со) eW», где k . гЬ (со) — arete 2Го) V(\ — Т2со2)2 + 42Г2ш2 ~ С 1 —ш2Г2 /V(to) = Для выявления характера АФЧХ определим N (со) и г]э (со) при некоторых частотах (табл. 2.4). АФЧХ колебательного звена изображен на рис. 2.14, г. Если АФЧХ звена определена экспериментально, то с ее помощью можно определить параметры k, £ и Т: коэффициент k равен длине отрезка на вещественной оси от начала координат до точки АФЧХ при со = 0; коэффициент £ находится из выражения А В = ft/2 : = = Ы1АВ; постоянная времени Т = 1/сот. Амплитудно-фазовые частотные характеристики САУ в разомкнутом состоянии Построение АФЧХ системы в разомкнутом состоянии, как и АФЧХ звеньев, выполняют в декартовой или полярной системах координат. При построении АФЧХ САУ в декартовой системе координат КПФ системы представляют в алгебраической форме Кр (/со) = Р (со) + + JQ (ю). Задаваясь различными значениями со, вычисляют Р (со) и Q (со) и откладывают их значения по осям координат. При построении АФЧХ в полярной системе координат КПФ системы представляют в показательной форме /Ср (/со) = N (со) е*64. Задаваясь различными значениями со, определяют N (со) и г]э (со) и откладывают их значения в полярной системе координат. Пример 1. Задана комплексная передаточная функция системы К (/со) =-М1+у»)-JN (ш) е/ЧЧЧ. Р(1 + Тф>) (1 - Тсо2 + 2£7усо) /со Определить выражения для модуля и аргумента КПФ. Пользуясь правилом, что модуль произведения комплексных чисел равен произведению их модулей, а аргумент — сумме аргументов сомножителей, находим: V 1 + T\v? V(l — Гш2)2 4 (27»2со $ (со) = arctg Г2(0 — arctg 7\со — arctg [2g7yo/(l — 7fcos)] — я/2. Для построения АФЧХ задаются различными значениями со, вычисляют значения N (со) и of (ш) и откладывают их в полярной системе координат. Соединение найденных точек дает АФЧХ системы. Пример 2. КПФ системы задана в следующем виде: к ,/Л = К (/«а)8 + fci/<o 4 62 kp. «о (/w)6 4 % (/со)4 -f- (/со)" + аз (/со)* + а4/со * Определим W (ю) и яр (со) КПФ: fc2 &[c02 + /&l(u t/i (со) + jVi (со) °зш2 4- / (а0ш6 — а2со8 + а4со) £/ (со) + /V (со) где TtV2 (со) + V2 (со) ! (со) = со; у (со)у(со) tV(co) =а1со4 — а3со2; ib (со) = arctg . --arctg ; , * w 6 (со)f/ (со) V (со) = а0со5 — + а4со. АФЧХ статической системы в разомкнутом состоянии. Пусть КПФ системы определяется выражением mп Кр (/со) = К П (1 + /сот;-)/ П (1 + /соГ,) - /V (со) е**", и > т. На частоте со = 0 : Kv (/со) = N (со) = йр; г]э (со) = 0, т. е. АФЧХ статической системы (рис. 2.15, а) начинается из точки, расположенной на вещественной оси и удаленной от начала координат на расстояние kv. При частоте со = со модуль N (со) = 0, поскольку п > >> т. Чтобы определить, под каким углом АФЧХ подходит к началу координат (сколько квадрантов проходит АФЧХ), нужно определить аргумент г]э (со) КПФ при со = со. Заметим, что каждый сомножитель первого порядка (1 + /со 7), стоящий в знаменателе, при со = со вносит запаздывание ф4 (со) = — arctg coTft = —90°, сомножитель в числителе — опережение, равное 90°. Поэтому при со=оо •ф (со) —<п90° + т90° = —(п — т) 90°. Если, например, п — т = = 3, то АФЧХ подходит к началу координат под углом, равным —270°, т. е. АФЧХ проходит три квадранта по часовой стрелке (рис. 2.15, а). В общем случае п — степень полинома знаменателя, т — степень полинома числителя. 0 ... 21 22 23 24 25 26 27 ... 143 |












