Раздел: Документация
0 ... 23 24 25 26 27 28 29 ... 143 Цо>) щ о к>1 1ды к<1 1ШБ 20 -20 -90°
Рис. 2.17. Логарифмические амплитудно-частотная l (со) и фа-зо-частотиая ф (со) характеристики пропорционального звена. 0,1110U Рис. 2.18. Логарифмические амплитудно-частотная l (со) и фазо-частотная ф (со) характеристики интегрирующего звена. Вцражение для ЛАЧХ звена: L (со) = 20 lg N (со) = 20 lg (А/ее) = 20 lg k — 20 lg со. (2.101) Из формулы (2.101) следует, что ЛАЧХ звена представляет сумму из двух слагаемых. Первое слагаемое 20 lg k не зависит от частоты и поэтому изображается прямой, проведенной параллельно оси частот на уровне 20 lg k (рис. 2.18). Второе слагаемое — 20 lg со зависит от частоты. Для определения вида графика, изображающего это слагаемое, зададимся несколькими частотами и определим ординаты графика при этих частотах:
Отмечаем точки А, В и С и проводим через них график. Из рисунка видно, что слагаемое — 20 lg со графически изображается прямой, проведенной под некоторым наклоном к оси частот (рис. 2.18). Под наклоном S ЛАЧХ понимается отношение приращения ординаты характеристики к приращению абсциссы: S = Д/. (co)/Ag со. Обычно в качестве Alg со берется отрезок на оси абсцисс, соответствующий октаве или декаде. Учитывая, что частоты, отстоящие друг от друга на 1 декаду, отличаются в 10 раз, наклон прямой —20 lg со: AL(co) Д lgco — 20 lg lOco — (— 20 lgco) = — 20 дБ/дек, Декада т. е. при увеличении со на декаду ордината L (со) убывает на 20 дБ. Для получения ЛАЧХ звена L (со) необходимо сложить ординаты графиков, изображающих слагаемые 20 lg k и — 20 lg со. Как видно из рисунка 2.18, где выполнено такое сложение, ЛАЧХ интегрирующего звена L (со) представляет собой прямую с наклоном —20 дБ/дек, имеющую при со = 1 ординату, равную 20 lg k. Опуская промежуточные операции, можно рекомендовать следующий порядок построения ЛАЧХ интегрирующего звена: 1) на частоте со = 1 отложить 20 lg k (точка Д); 2) через точку Д провести прямую с наклоном —20 дБ/дек. Для этого от точки Д вправо отложить декаду (точка Е) и от точки Е отложить вниз 20 дБ (точка F); 3) провести прямую через точки Д к F. Эта прямая и будет ЛАЧХ интегрирующего звена. Частоту соА, при которой ЛАЧХ пересекает ось частот, найдем из уравнения L (щ) = 20 lg k — 20 lg cofc = 0 : coft = k. Используя это, можно рекомендовать еще одно правило построения ЛАЧХ звена: на оси абсцисс (частот) отметить точку, соответствующую частоте coft = = k, и через эту точку провести прямую с наклоном —20 дБ/дек. При изменении k наклонная прямая перемещается в вертикальном направлении параллельно себе. Если k = 1, то 20 lg k = 0 и выражение для ЛАЧХ звена примет вид L (со) = —20 lg со, т. е. в этом случае ЛАЧХ пересечет ось 0 дБ при coft = 1 (наклонная прямая ABC, рис. 2.18). Выражение для ЛФЧХ интегрирующего звена: ф (со) =■—я/2, откуда видно, что аргумент комплексной передаточной функции звена не зависит-от частоты и поэтому ЛФЧХ звена представляет прямую, параллельную оси частот, проведенную на уровне — 90°. Логарифмические частотные характеристики идеального дифференцирующего звена. Комплексная передаточная функция звена: К (/со) = /сот = соте/я/2 = N (со) ета\ где N (со) = сот; я]> (со) = я/2. Выражение для ЛАЧХ звена: L (со) = 20 lg N (со) = 20 lg сот = 20 lg т + 20 lg со. Слагаемое L, (со) = 20 lg т не зависит от частоты и поэтому изображается прямой, параллельной оси абсцисс на уровне 20 lg т (прямая L, (со), рис. 2.19). Слагаемое L2 (со) =201gco изображается прямой с наклоном 20 дБ/дек. Поскольку 20 lg со =0 при со = 1, прямая L2 (со) пересекает ось 0 дБ в точке, соответствующей частоте со = 1. ЛАЧХ звена L (со) получается сложением ординат слагаемых Lx (со) и L2 (со). Из рис. 2.19 видно, что ЛАЧХ идеального дифференцирующего звена L (со) представляет собой прямую с наклоном 20 дБ/дек, имеющую при со = 1 ординату, равную 20 lgx. Частоту cofc, при которой ЛАЧХ L (со) звена пересекает ось частот, найдем из уравнения 20 lg щх = 0: соАт = 1, откуда щ ~ 1/т. Чтобы построить ЛАЧХ идеального дифференцирующего звена, следует на оси частот отметить точку, соответствующую частоте щ = = 1/т, и через нее провести прямую под наклоном 20 дБ/дек. Выражение для ЛФЧХ звена ф (со) = я/2, т. е. ЛФЧХ идеального дифференцирующего звена — прямая, параллельная оси абсцисс, проведенная на уровне я/2 (см. рис. 2.19). во 20lgk 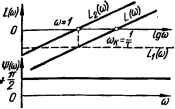 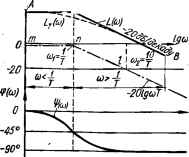 Рис. 2.19. Логарифмические амплитудно-частотная L (со) и фазо-ча-стотная ф (со) характеристики идеального дифференцирующего звена. Рис. 2.20. Логарифмические амплитудно-частотная L (со) и фазо-частотная ф (со) характеристики апериодического звена. Логари мические частотные характеристики апериодического звена. Комплексная передаточная функция звена: , + ушГ у j + ы2г2 е= TV (со>е Выражение для ЛАЧХ звена: L (со) = 20 lg N (со) = 201g (k/yi+im = 201g ft — 201g Л + со2Г2. (2.102) Для области низких и высоких частот выражение для L (со) может быть упрощено. В области малых со, где со 1/Т, имеем 1 > со2Г2 н поэтому V\ + со2Г2 « 1. Учитывая, что lg 1 =0, выражение (2.102) для L (со) в рассматриваемом диапазоне частот будет иметь вид: L(co) = 201g/e,(2.103) т. е. ЛАЧХ апериодического звена в области низких частот представляет прямую, проведенную на уровне 20 lgfe параллельно оси частот (отрезок АС рис. 2.20). В области высоких частот, где со 1/Т, имеем 1 соГ2, поэтому у"\ + со2Г2 « соТ и выражение (2.102) будет иметь вид: L(co) = 20 lg — 201gcoT.(2.104) Первое слагаемое 20 lg графически изображается прямой, параллельной оси абсцисс (на рис. 2.20 прямая проведена пунктиром). Для определения вида графика второго слагаемого —20 lg соТ зададимся несколькими частотами и определим ординаты для этих частот: coj = 1/Т; cojT =1; — 20 lgcoiT" = 0 дБ (точка п); со2= 10/7; со2Т -. 10; — 201gmar=* -20 дБ (точка /). Проводим через точки п, I прямую. Как видим, слагаемое —20 lgco7* изображается прямой с наклоном: = ДМсо) = -201gl0cor-(-201gcor) =g Д lg содек" 0 ... 23 24 25 26 27 28 29 ... 143 |












