Раздел: Документация
0 ... 26 27 28 29 30 31 32 ... 143 Логарифмические ФЧХ отдельных звеньев и системы изображены на рис. 2.24 кривыми с индексами в соответствии с приведенной выше таблицей. ЛФЧХ системы (со) в области низких частот начинается со значений — (n/2)v, где v — порядок астатизма системы. Из рис. 2.24 видно, что если в некоторой области частот наклон ЛАЧХ системы L (со) сохраняет постоянное значение, то и ЛФЧХ системы гр (со) в этой области частот остается почти постоянной. В области низких частот, где наклон ЛАЧХ постоянен и равен —20 дБ/дек, кривая (со) также неизменна и равна —90°. По мере приближения к первой частоте сопряжения ы1 = 1/7\, где наклон ЛАЧХ увеличивается до —40 дБ/дек, фазовая характеристика начинает изменяться все более быстро, стремясь к новому постоянному значению, равному —180°. Поскольку имеется еще одна частота сопряжения со2 = 1/Та, на которой наклон ЛАЧХ становится равным —60 дБ/дек, фазовая характеристика снова начинает резко изменяться в области этой частоты сопряжения, стремясь к значению —270°. Построение логарифмической амплитудно-частотной характеристики по коэффициентам передаточной функции. Часто выражение передаточной функции сложной системы получается не в виде дроби, числитель и знаменатель которой представляют собой произведения передаточных функций элементарных звеньев, а в виде отношения полиномов (см., например, формулу (2.77)). Чтобы построить ЛАЧХ по передаточной функции, представленной в виде отношения полиномов, можно эти полиномы разло- жить на элементарные множители и для построения характеристики использовать рассмотренный выше метод. Однако при этом необходимо вычислять корни уравнений, получающихся приравниванием нулю полиномов числителя и знаменателя передаточной функции. Это усложняет процесс построения. В рассматриваемом случае построение ЛАЧХ удобнее выполнить непосредственно по коэффициентам полиномов передаточной функции. Убедимся в возможности такого построения на примере системы, состоящей из последовательно включенных двух апериодических и интегрирующего звеньев: Кр (р) = kjp (Тгр -f- 1)(Т2р -f- 1). Асимптотическая ЛАЧХ такой системы представляет собой ломаную, имеющую изломы при частотах сопряжения g>i = 1/Тг и со2 = 1/Гг. Низкочастотная асимптота имеет наклон — 20 дБ/дек н проходит через точку с координатами со = 1; L (со) = 20 Ig kp. Раскроем скобки в выражении для передаточной функции *р (Р) = р \TxTj? + (7\ + Т2) р + 1] = р (а + alP + а2) где а0 = TtTs; ах = Тг + Т2; а2 = 1. Определим отношения коэффициентов с большими индексами к коэффициентам с меньшими индексами: а21ах = l/ + Т2); aja, = (Tf + Т2)1Т{Г2. Если при записи передаточной функции принимаются 7\ > Ts, то можно написать следующие приближенные равенства: aja \lTl = аг/а0 « l/T2 — сог. Таким образом, значения частот сопряжения ЛАЧХ могут быть приближенно определены как отношения коэффициентов передаточной функции. Данный метод построения ЛАЧХ может быть распространен также на более общий случай, когда передаточная функция системы имеет вид: Кр(р) = -—7-т=г--—-— . »i<n; n = fe + v. (а0рк + а1рк 1+ ••• +ak lp + ak)pv Определяются частоты сопряжения: числителя bm/bm l = to,; bm l/bm 2 = w2, . . . ; 6j/*o = am, знаменателя aft/aft , = coj; ak l/ak 2 = toa; . . . ; aj/a,, = coft и их значения по мере роста откладываются по оси частот. Наклон ЛАЧХ на частотах сопряжения, принадлежащих знаменателю, изменяется на —20 дБ/дек, а на частотах сопряжения, принадлежащих числителю, на +20 дБ/дек. Низкочастотная асимптота проводится под наклоном —20v дБ/дек через точку с координатами (ш = 1; L (to) = 20 lg kp). ГЛАВА 3 Устойчивость систем автоматического управления 3.1. Понятие и условие устойчивости САУ Определение устойчивости САУ Следящая система (рис. 1.14, а) находится в состоянии равновесия, когда ее ошибка е (t) = 0. Это состояние может быть устойчивым или неустойчивым. Если после некоторого изменения задающего воздействия a (t) (поворота ведущего вала на угол а„) система в результате затухающего переходного процесса (рис. 2.1, а, б) снова приходит в состояние равновесия е (t) = 0, то это состояние равновесия является устойчивым и система называется устойчивой. Когда после незначительного изменения задающего воздействия (отклонения системы от равновесного состояния) система не стремится в первоначальное состояние равновесия, а в ней возникают незатухающие колебания управляемой величины р (0 (рис. 2.1, в, г) или же изменение р (f) будет независимым от a (t), то состояние равновесия в данной системе является неустойчивым и система называется неустойчивой. Наглядное представление об устойчивом и неустойчивом равновесных состояниях дает рассмотрение системы шар — поверхность. Шар, помещенный во впадине (рис. 3.1, а), находится в устойчивом равновесном состоянии, так как после его отклонения под влиянием внешнего воздействия он возвратится в свое первоначальное состояние. Система шар — поверхность является устойчивой. Шар, расположенный на верхней точке возвышенности (рис. З.1., б), находится в неустойчивом равновесном положении: достаточно незначительного отклонения от Рис. 3.1. К понятию устойчивости равиовес ных состояний системы шар—поверхность: а — устойчивое состояние; б — неустойчивое состо яиие; в — состояние, устойчивое при малых и неус тойчивое при больших отклонениях. 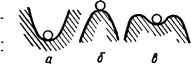 этого состояния, и шар скатится по склону поверхности и не возвратится в исходное положение. Рассматриваемая система неустойчива. Таким образом, под устойчивостью понимается свойство системы возвращаться в прежнее состояние равновесия после вывода ее из этого состояния и прекращения изменения задающего или влияния возмущающего воздействия. Только устойчивая система является работоспособной. Поэтому одной из основных задач теории автоматического управления является исследование устойчивости САУ. Основы строгой теории устойчивости динамических систем были разработаны акад. А. М. Ляпуновым в работе «Общая задача об устойчивости движения» (1892 г.). Понятия об устойчивости, вытекающие из этой работы, заключаются в следующем. Если система описывается линейным дифференциальным уравнением, то ее устойчивость не зависит от величины возмущения. Линейная система, устойчивая при малых возмущениях, будет устойчива и при больших. Нелинейные же системы могут быть устойчивы при малых возмущениях и неустойчивы при больших. Примером такой нелинейной системы являются стенные часы. Если неподвижному маятнику сообщить слабый толчок, то маятник, совершив несколько качаний, остановится, т. е. система устойчива при малых возмущениях. Если же маятнику сообщить более сильный толчок, то последний у заведенных часов начинает совершать незатухающие колебания. Следовательно, система неустойчива при больших возмущениях. Наглядное представление о нелинейных системах, устойчивых при малых и неустойчивых при больших возмущениях, дает рассмотрение шара, помещенного во впадине, расположенной на вершине выпуклого тела (рис. 3.1, в). При малых отклонениях, не превышающих края впадины, шар возвращается в исходное положение, т. е. система шар—поверхность устойчива. При отклонениях за край впадины шар не возвращается в исходное положение — система неустойчива. Поэтому для нелинейных систем устойчивость исследуется отдельно для случая малых возмущений, т. е. устойчивость в малом, и устойчивость при больших возмущениях, т. е. устойчивость в большом. Согласно теореме Ляпунова, об устойчивости нелинейных систем при малых возмущениях можно судить по их линеаризированным уравнениям, достаточно точно описывающим поведение систем при малых отклонениях от состояния равновесия. Для определения устойчивости нелинейных систем при больших возмущениях необходимо пользоваться исходными нелинейными уравнениями динамики. В большинстве практических случаев системы, устойчивые при малых отклонениях, оказываются устойчивыми и при достаточно больших отклонениях, возможных в процессе эксплуатации, и поэтому вопрос об устойчивости этих систем может быть решен на основании исследования линеаризованных уравнений. Проблема устойчивости обычно возникает в замкнутых САУ из-за влияния обратной связи. Поэтому в дальнейшем устойчивость исследуется на примерах замкнутых систем, хотя методы исследования устойчивости универсальны. 0 ... 26 27 28 29 30 31 32 ... 143 |












