Раздел: Документация
0 ... 29 30 31 32 33 34 35 ... 143 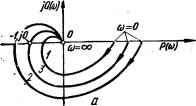 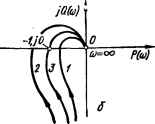 Рис. 3.3. Амплитудно-фазовые частотные характеристики САУг а — статистических; б — астатических. дующим образом: система автоматического управления, устойчивая в разомкнутом состоянии, будет устойчива в замкнутом состоянии, если АФЧХ разомкнутой системы не охватывает точку на комплексной плоскости с координатами (—1, /О). На рис. 3.3 показаны АФЧХ статических и астатических систем. Амплитудно-фазовые характеристики / не охватывают критическую точку, поэтому системы с такими характеристиками устойчивы. Амплитудно-фазовые частотные характеристики 2 охватывают точку (—1, /О), поэтому системы 2 неустойчивы. Амплитудно-фазовые частотные характеристики 3 проходят через критическую точку; соответствующие системы находятся на границе устойчивости. Приведем доказательство критерия. Если передаточная функция системы в разомкнутом состоянии Kv (р) =D (p)lF (р), то передаточная функция замкнутой системы Ka (р) =D {p)i[F (р) + D (р)] =D {p)l I F3 (/>). гДе F3 (p) = F (p) + D (p). Рассмотрим функцию F3(P)/F(p) = f{p),(3.8) т. е. отношение характеристического полинома замкнутой системы к характеристическому полиному разомкнутой системы. Числитель и знаменатель выражения (3.8) можно представить так: F3(P) (Р~ Pi) (Р —Ра) (Р —Рз) ■ • ■ (Р- f(p) = F{p) (р — р\) (р — р9) (р — р3) Рп) (р-р„) где р2, р„ — корни характеристического уравнения замкнутой системы; р\, р2, рп — корни характеристического уравнения разомкнутой системы. Подставляя /со вместо р в последнее выражение, получим F3 (/со) (/со — р,) (/со — р2) ... (/со — рп) F (/о) (;ш — рх) (/и — р2) . . . (/и — Р„) При разработке критерия устойчивости задача состоит в определении условий, при которых все корни характеристического уравнения замкнутой системы лежат слева от мнимой оси комплексной плоскости. На комплексной плоскости каждый из корней р/ и р) изображается точкой (см. рис. 3.2) или вектором, проведенным из начала координат в соответствующую точку (рис. 3.4, а). Текущая координата /со< гео- Put aS Рис. 3.4. Векторное изображение на комплексной плоскости корней характеристического уравнения, текущих координат /coj, сомножителей (/со — pj) (а) и определение угла поворота , вектора (/со — pi) при изменении со от 0 до со. метрически также изображается вектором, направленным из начала координат вдоль мнимой оси. Каждый сомножитель (/со— pj) или (/со — pj), являющийся разностью двух векторов, представляет собой также вектор, начало которого находится в точке, соответствующей корню р} или р), а конец — в точке /со* на мнимой оси /со. При изменении /cof концы разностных векторов будут перемещаться вдоль мнимой оси, а сами векторы поворачиваться. Принято считать поворот вектора против часовой стрелки положительным. При изменении со от —оо до + оо каждый разностный вектор числителя (/с° — Pi) и знаменателя (/со — pj), начало которого (т. е. соответствующий корень) лежит в левой полуплоскости, повернется на угол я, в каждый вектор, начало которого находится в правой полуплоскости, — на — я. На практике ограничиваются изменением со от 0 до со. При этом, если р/ (или р/) — корень действительный отрицательный, то при изменении со от 0 до оо вектор (/со — pj) повернется на угол + я/2. Если среди корней имеются два комплексных корня рм+i = а ± /Q, расположенных, например, как показано на рис. 3.4, б,то при изменении со от 0 до со вектор (/to — pj) повернется на угол я/2 + р\ а вектор (/со — Pf+i) на угол я/2 — р. Сумма углов поворота этих двух векторов равна 2я/2. Таким образом, можно считать, что при изменении со от 0 до со каждый разностный вектор числителя (/со — pj) и знаменателя (/со — — Pl) поворачивается на л/2 или —я/2 в зависимости от того, где лежит соответствующий корень. Поскольку функции F3 (/со) и F (/со) равны произведению элементарных векторов, то и сами эти функции являются векторами, аргументы которых равны сумме аргументов соответствующих разностных векторов: argOto) = arg(/co — pt)+ ••• + arg(/co —р„), arg F (/со) = arg (/со — p\) + • • • + arg (jti> — pn). •Результирующее изменение arg F3 (/to) и arg F (/со) при изменении со от 0 до оо зависит от расположения соответствующих корней на ком- плексной плоскости. Предположим, что разомкнутая система устойчива (устойчивость разомкнутой системы часто можно определить без всяких вычислений непосредственно по схеме системы; например, разомкнутая система, состоящая из устойчивых звеньев и не содержащая местных обратных связей, заведомо устойчива). В этом случае корни pi находятся в левой полуплоскости и изменение аргумента F (/со) (поворот характеристического вектора разомкнутой системы) при изменении со от 0 до + оо равно A arg F (/со) =* пп/2, где п — степень характеристического уравнения разомкнутой системы F (р) = = 0. Изменение аргумента F3 (/со) при изменении со от 0 до + оо в общем случае равно A arg F3 (/со) = (п — /) я/2 — /я/2 = (п — 21) я/2, где / — число корней в правой полуплоскости. Изменение аргумента / (/со) равно разности изменений аргументов числителя и знаменателя: Д arg / (Ja) — Д arg F3 (/со) — arg F (/со) = (n — 21) я/2 — ля/2 = — In. Система будет устойчива, если / =0, т. е. если Д arg/ (/со) =0. Вектор / (/со) при изменении со от 0 до + оо опишет угол, равный нулю, лишь в том случае, если годограф этого вектора не охватывает начала координат (рис. 3.5, а). От годографа / (/со) легко перейти к годографу Кр (/с°)« т- е- к АФЧХ разомкнутой системы. Действительно, выражение для / (/со) можно записать в следующем виде: где Кр 0<°) — комплексная передаточная функция разомкнутой системы. Геометрически последнее выражение иллюстрируется на рис. 3.5, а. Таким образом, годограф вектора / (/со) представляет АФЧХ разомкнутой системы, но сдвинутую вправо на единицу. Поскольку удобнее пользоваться амплитудно-фазовой частотной характеристикой, а не годографом вектора / (/со), то перенесем ось координат вправо на единицу, как показано на рис. 3.5, б. Изменение аргумента / (/со) при изменении со от 0 до + со будет равно нулю, если точка (—1, /О) находится вне амплитудно-фазовой частотной характеристики разомкнутой системы. Отсюда следует формулировка частотного случая критерия устойчивости Найквиста — Михайлова: система автоматического управления, 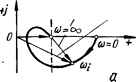 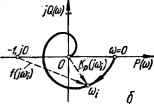 Рис. 3.5. Годограф вектора f (jco) (а) и АФЧХ равомкиутой системы (б). 0 ... 29 30 31 32 33 34 35 ... 143 |












