Раздел: Документация

0 ... 30 31 32 33 34 35 36 ... 143

a=0 f,/0 (
	<y=ooj P(to)
	a

ш	•
	/"N. (0=0
V b)=oo	в

Рис. 3.6. АФЧХ устойчивых и неустойчивых систем, имеющих / корней характеристического уравнения в правой полуплоскости:

0— устойчивой системы (/ = 1); б — устойчивой системы (/ = 2); в — неустойчивой системы (/ = 2).

устойчивая в разомкнутом состоянии, будет устойчива в замкнутом состоянии, если АФЧХ разомкнутой системы не охватывает критическую точку (—1, /О).

Если система в разомкнутом состоянии неустойчива (например, имеются звенья, охваченные положительной обратной связью), то при определенных условиях замкнутая система может быть устойчивой. В этом случае изменение аргумента характеристического вектора разомкнутой системы F (/со) при изменении со от 0 до + со равно Л arg F (/со) = (л — 21) я/2, где / — число корней характеристического уравнения разомкнутой системы в правой полуплоскости.

Если замкнутая система устойчива, то A arg F3 (/со) = яя/2, тогда A arg / (/ю) = пп/2 — (я — 21) я/2 = (1/2) 2я, т. е. система автоматического управления, неустойчивая в разомкнутом состоянии и имеющая

1корней в правой полуплоскости, будет устойчива в замкнутом состоянии, если АФЧХ разомкнутой системы охватывает критическую точку (—1, /О) 1/2 раз в положительном направлении при изменении частоты со от О до со. На рис. 3.6, а, б, в показаны АФЧХ устойчивых и неустойчивых систем для различных /.

Системы, неустойчивые в разомкнутом состоянии, включают в себя неустойчивые звенья. Рассмотрим неустойчивые апериодическое и колебательное звенья.

Неустойчивое апериодическое звено описывается передаточной функцией К (р) = k/(Tp — 1) или КПФ К (/со) = k/(j(oT — 1) = Р (со) + + JQ (со), где Р (со) = —Ш + (со7?]; Q (со) = — соШИ + (соГ)2]. АФЧХ звена изображена на рис. 3.7, а.

Неустойчивое колебательное звено (I < 0) имеет передаточную функцию К(р) = k/{T*p* — 2%Тр + 1), откуда КПФ

К (/со) = k/(\ — Т2со2 — /2£Гсо) = Р (со) -f- JQ (со),

где

fe(I-ГУ)

гУ»)— (1 — rto*)2 + (217-cd)2

Q(co)

2k%T(u

(1 — г2со2) + (2£7Чо)2

АФЧХ звена изображена на рис. 3.7, б.

Понятие об условной устойчивости многокоитурных систем. Правило о числе переходов амплитудно-фазовых частотных характеристик. Для повышения точности в системы включают различные корректи-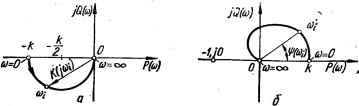

---

Рис. 3.7. АФЧХ неустойчивых звеньев: а — апериодического; 6 — колебательного.

рующие устройства. Амплитудно-фазовые частотные характеристики таких систем могут иметь сложную форму. Часто АФЧХ пересекают вещественную ось и справа и слева от критической точки (—1, /О) (рис. 3.8). Такие системы с клювообразной АФЧХ называются системами условно устойчивыми, или системами Второго рода (обычные системы называют системами первого рода).

Система, устойчивая в разомкнутом состоянии, АФЧХ которой в разомкнутом состоянии не охватывает точку (—1, /О), устойчива в замкнутом состоянии. Вывести данную систему из устойчивости, в отличие от системы первого рода, можно не только увеличением коэффициента усиления разомкнутой системы, но и его уменьшением.

При определении устойчивости систем с клювообразными и более сложными по форме АФЧХ практически удобнее пользоваться правилом о числе переходов, вытекающим из критерия устойчивости.

Рассмотрим наиболее распространенный случай, когда САУ в разомкнутом состоянии устойчива. Будем считать переход АФЧХ через вещественную ось снизу вверх отрицательным, а сверху вниз — положительным. Направление движения по АФЧХ при этом принимаем совпадающим с направлением возрастания со. С учетом сделанного замечания правило о числе переходов можно сформулировать следующим образом: система автоматического управления, устойчивая в разомкнутом состоянии, будет устойчива в замкнутом состоянии, если разность между числами положительных и отрицательных переходов АФЧХ разомкнутой системы через отрезок (—со, —вещественной оси равна нулю.

Физический смысл амплитудно-фазового критерия устойчивости. Физический смысл амплитудно-фазового критерия для систем первого рода, устойчивых в разомкнутом состоянии, можно объяснить следующим образом. Система автоматического управления обычно (см., например, рис. 2.4) содержит апериодические, колебательные и интегрирующие звенья, которые вносят запаздывание колебаний по фазе. Запаздывания, вносимые апериодическим и колебательным звеньями, согласно выражениям для аргументов комплексных передаточных функций этих звеньев:

% («о) = — arctg 7>; яр* (со) = — arctg [2£7>/(1 — 7*со2)].

с увеличением частоты увеличиваются. Из-за этого колебания на выходе разомкнутой системы (рис. 3.9, а) будут отставать по фазе относительно колебаний 6 (г) на входе. С увеличением частоты, согласно приве-

---

Щи»	V
	)&)=oo a=
	0 J

Plu»

Рис. 3.8. АФЧХ условно устойчивой системы

Рис. 3.9. Структурная схема (а), АФЧХ (б) и формы колебаний на входе и выходе разомкнутой системы (в).

ceft).

эс

1	№

£o.c(t)

!Ё1

денным выражениям, это отставание увеличивается и на определенной частоте соя колебания р" if) будут отставать от колебаний 9 (г) на 180° (рис. 3.9, б, в). Колебания ро.с (£) на выходе отрицательной обратной связи (рис. 3.9, а) на этой частоте будут совпадать по фазе с колебаниями 9 (f) на входе системы (рис. 3.9, в). Благодаря этому на частоте со„ обратная связь из отрицательной превращается в положительную.

Если на частоте со„ модуль N (со„) КПФ разомкнутой системы равен или больше единицы (N (со„) ;> 1), т. е. если амплитуда Рт выходных колебаний системы будет равна амплитуде колебаний на входе или больше ее, то при замыкании системы в ней возникнут соответственно либо незатухающие, либо возрастающие колебания, т. е. система будет неустойчива.

Если модуль N (соя) < 1, т. е. если при прохождении через прямой канал системы сигнал ослабляется и амплитуда Рт колебания на выходе будет меньше, чем на входе 9т, то колебания в замкнутой системе затухнут, так как на вход системы с выхода обратной связи каждый раз будет поступать колебание все меньшей амплитуды. Система в этом случае будет устойчива.

Запас устойчивости по модулю и по фазе. Система находится на границе устойчивости, если ЛГр (со„) = Pm/6m =1. Под коэффициентом запаса устойчивости по модулю понимают отношение о = Л/гр (соя)/Л (со„) = l/N (соя) = 1/ОВ,

где ОВ — расстояние между началом координат и точкой пересечения АФЧХ с вещественной осью (рис. 3.10, а). Коэффициент о показывает, во сколько раз можно увеличить модуль N (со„) КПФ разомкнутой системы, чтобы замкнутая система пришла к границе устойчивости. При а > 1 система устойчива, при а = 1 — находится на границе устойчивости, при а < 1 — неустойчива.

Иногда коэффициент запаса устойчивости по модулю выражают в децибелах:

а = 20 lg [ l/N (со„)] = 20 lg (1/ОВ).

0 ... 30 31 32 33 34 35 36 ... 143