Раздел: Документация
0 ... 32 33 34 35 36 37 38 ... 143 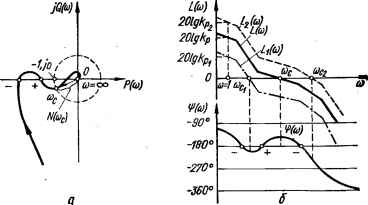 Рис. 3.15. Частотные характеристики условно устойчивой системы: а — АФЧХ; б — ЛЧХ; L (<g), (ю), £, (ю) — ЛАЧХ при различных коэффициентах усиления (ftp, < ftp2 < *рз); (й>) — ЛФЧХ системы. Запас устойчивости по амплитуде о определяется как число децибел, на которое нужно увеличить усиление системы, чтобы система достигла границы устойчивости. Запас устойчивости по фазе у определяется как разность между 180° и абсолютным значением аргумента КПФ при частоте среза сос, т. е. v = 180° — ip (сос). Определение запаса устойчивости по амплитуде и по фазе показано на рис. 3.14, Для систем с клювообразными и более сложными по форме АФЧХ практически удобнее пользоваться формулировкой логарифмического частотного критерия устойчивости, вытекающей из правила о числе переходов. На рис. 3.15, а изображена АФЧХ условно устойчивой системы, а на рис. 3.15, б — логарифмическая амплитудная L (со) и логарифмическая фазочастотная я]) (со) характеристики, соответствующие этой АФЧХ. Отрицательным переходам АФЧХ через отрицательную вещественную ось снизу вверх будут соответствовать переходы логарифмической ФЧХ через линию — 180° сверху вниз, которые будем считать также отрицательными. Положительным переходам АФЧХ через отрицательную вещественную ось сверху вниз будут соответствовать переходы ЛФЧХ через линию —180° снизу вверх. Принимая во внимание, что при N (со) >» 1 ЛАЧХ положительна, логарифмический критерий устойчивости на основании правила о числе переходов можно сформулировать следующим образом: система, устойчивая в разомкнутом состоянии, будет устойчива в замкнутом состоянии, если разность между числами положительных и отрицательных переходов фазочастотной характеристики через прямую —180° равна нулю в диапазоне частот, в котором логарифмическая амплитудно-частотная характеристика положительна. Логарифмические амплитудно- и фазочастотные характеристики L (со), ф (со), изображенные на рис. 3.15, б, соответствуют устойчивой системе. На том же рисунке ЛАЧХ Lx (со) и L2 (со) той же системы, но с меньшим (&pi) и большим (&р2) коэффициентом усиления соответствуют неустойчивому режиму системы. С помощью критериев устойчивости можно определить, устойчива ли система при заданных ее параметрах (постоянных времени, коэффициентах усиления). Однако при проектировании САУ часто ставится вопрос по-иному: заданы все параметры системы, за исключением одного или двух, которые могут изменяться в широких пределах; требуется определить, при каких значениях этих параметров система устойчива. Некоторые параметры системы могут изменяться также в процессе эксплуатации. Поэтому важно знать, сохранит ли система устойчивость при возможных изменениях этих параметров. Поставленные задачи могут быть решены, если установить область возможных изменений тех или иных параметров (или коэффициентов характеристического уравнения) системы, при которых еще не нарушается ее устойчивая работа. Для построения областей устойчивости разработаны специальные методы: метод диаграмм Вышнеградского и метод D-разбиений. ГЛАВА 4 Качество систем автоматического управления 4.1. Показатели качества систем автоматического управления Как было выяснено в предыдущей главе, система автоматического управления должна быть устойчивой. Однако требование устойчивости является для САУ еще недостаточным. Система может быть устойчивой, т. е. ее переходный процесс носит затухающий характер, но время затухания настолько велико или ошибка в установившемся режиме настолько большая, что практически данная система не может быть использована. Поэтому система должна быть не только устойчивой, но и иметь определенный переходный процесс, а ее ошибки в установившихся режимах не должны превышать допустимых. Характер переходного процесса линейной системы в отличие от устойчивости зависит не только от параметров системы, но и от вида возмущающего (задающего) воздействия и начальных условий. Чтобы сравнивать системы по характеру переходного процесса, из возможных воздействий выбирают типовые или наиболее неблагоприятные и определяют кривую переходного процесса при нулевых начальных условиях. В качестве типовых воздействий обычно принимают единичное ступенчатое воздействие, единичный импульс, линейно возрастающее воздействие, синусоидальное воздействие и др. Для большинства систем типовым и наиболее неблагоприятным является воздействие вида единичной ступенчатой функции a{t) =1 (f) (см. рис. 2.2, б). Реакция системы на единичное ступенчатое воздействие при нулевых начальных условиях, как известно, называется переходной функцией системы. Для следящих систем обычно рассматривают переходную функцию 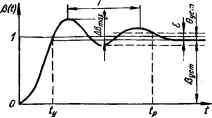 Рис. 4.1. Определение показателей качества системы по кривой переходного процесса. h (г), вызванную изменением задающего воздействия a (f), а для систем стабилизации — переходную функцию fiL (f), вызванную изменением возмущающего воздействия L (t). Переходная функция системы оценивается с помощью совокупности характеристик, называемых показателями качества переходного процесса. Обычно различают следующие показатели качества переходного процесса системы. Время регулирования, или время переходного процесса, tp — время, по истечении которого отклонение управляемой величины В (г) относительно установившегося значения 6уст становится и остается по аб? солютному значению меньше наперед заданной величины е (рис. 4.1). Обычно принимается е = 0,05Вуст. Время регулирования характеризует быстроту затухания переходного процесса. Время установления ty — промежуток времени, за который управляемая величина в первый раз достигает своего установившегося значения; ty характеризует скорость процесса управления. Перерегулирование а — выраженное в процентах отношение максимального отклонения управляемой величины АРтах от своего установившегося значения Вуст к Вуст: О = (ЛРтах/Руст) 100. Число п и частота f колебаний управляемой величины в течение времени переходного процесса. Показатели качества переходного процесса дают представление о поведении системы только в переходном режиме, т. е. об изменении переходной составляющей ошибки. Точность же системы в установившихся режимах оценивается с помощью статических и динамических ошибок, т. е. ошибок системы в установившихся режимах. Эти установившиеся ошибки по аналогии можно назвать показателем качества системы в установившихся режимах. Совокупность показателей качества переходного процесса и установившихся режимов называется показателями качества системы. Рассмотренные показатели называются прямыми показателями качества системы. Считается, что система обладает требуемым качеством, если ее показатели качества не превышают заданных значений, определенных назначением системы. Одной из основных задач рационального выбора схемы системы и ее параметров является обеспечение того, чтобы время регулирования, перерегулирование и установившаяся ошибка не превосходили заданных величин. Если известно уравнение замкнутой системы (см., например, выражение (3.1)), то переходную функцию р (t) можно найти путем решения этого уравнения. Более простой метод определения переходной функции основан на использовании операционного исчисления — метод разложения изображения переходной функции (или ошибки) системы на элементарные дроби. 0 ... 32 33 34 35 36 37 38 ... 143 |












