Раздел: Документация
0 ... 34 35 36 37 38 39 40 ... 143 4.3. Частотный метод анализа качества переходных процессов систем автоматического управления Обоснование возможности использования частотных характеристик САУ для построения кривой переходного процесса В отличие от анализа устойчивости САУ, когда обычно неходят нз ее частотных характеристик в разомкнутом состоянии, при анализе качества переходных процессов пользуются.частотными характеристиками замкнутой системы. Зная частотную характеристику замкнутой системы Кз (/<*>) = W3 (со) е*8*, можно определить ее выходную величину при подаче на вход гармонического воздействия. Действительно, если на вход следящей системы подано гармоническое задающее воздействие a (/) = ■= ат sin со/, комплексное изображение которого а = ате,ш, то в установившемся режиме комплексное изображение выходной величины Р = К3 т «me>™ = *з (со) ее*» = +\ где Pm = N3 (со) «т, ф3 (со) — амплитуда и сдвиг по фазе выходных колебаний со-ответствеиио. С помощью частотной характеристики замкнутой системы можно не только определить выходную величину системы в установившемся режиме при гармоническом входном воздействии, но и найти реакцию системы в переходном процессе на произвольное воздействие а (/). Действительно, представляя это воздействие в зависимости от того, является оно периодической или непериодической функцией, в виде ряда или интеграла Фурье, т. е. в виде бесконечной суммы гармонических колебаний, можно по частотной характеристике определить реакцию системы на каждое из этих элементарных колебаний, а затем, просуммировав все реакции, найти результирующую реакцию в виде суммы или интеграла. Найдем реакцию системы на единичную ступенчатую функцию (т. е. найдем переходную функцию системы), используя частотную характеристику системы. Как известно, интеграл Фурье для единичной ступенчатой функции имеет вид: 001 2я J /со —оо т. е. единичная ступенчатая функция может быть представлена как бесконечная сумма элементарных колебаний вида <Лве/й)/2я/со. Каждому из этих колебаний соответствует выходное колебание К3 (/со) <2сое/<в/2я/со, а реакция системы на единичную ступенчатую функцию выражается суммой оо ею = -5Г 1 *•</»>-тйг*0-<4-9> —оо Представляя /ГзО03) в алгебраической форме Къ (/ю) = Р3 (оз) + /Q3 (со) и преобразуя выражение (4.9), получаем следующую формулу для переходной функции: оо Р (/) = А Г Рз(0)) sin ю№,(4.10) я J со о где Р3 (to) — вещественная частотная характеристика (ВЧХ) замкнутой системы. Полученное выражение связывает ВЧХ системы с ее переходной функцией. Таким образом, при частотном методе, анализа косвенной характеристикой качества является вещественная частотная характеристика замкнутой системы. Связь между показателями качества переходного процесса в вещественной частотной характеристикой замкнутой системы Предварительно дадим некоторые определения, связанные с вещественной частотной характеристикой, возможный вид которой показан на рис. 4.3. Интервал частот 0 < со to„, в котором P3 (to) > 0, называется интервалом положительности; частота <оп, при которой ВЧХ Р3 (to) впервые переходит нз положительной области в отрицательную,— частотной положительности. Интервал частот 0 < со сос ч на-вывается интервалом существенных частот, если при со > to0 ч величина Р3 (to) j 6. Обычно 6= (0,1...0,2) Р3 (0). Влияние части частотной характеристики, где to > сосч, на качество системы несущественно и им можно пренебречь. Отбрасываемый «воет» влияет на начальную часть переходного процесса. Начало же вещественной характеристики определяет главным образом конечную часть переходного процесса. Одним из основных вопросов любого косвенного метода анализа качества является установление связи между выбранной косвенной характеристикой качества и показателями качества. На основании анализа выражения (4.10) установлена следующая зависимость показателей качества от вида вещественной частотной характеристики замкнутой системы [64]. 1.Чтобы перерегулирование не превышало 18 % (а 18 %), достаточно иметь положительную невозрвстающую вещественную частотную характеристику (рис. 4.4, кривая 1). 2.Для обеспечения монотонности переходного процесса достаточно, чтобы производная dPB (co)/dco представляла собой отрицательную убывающую по модулю функцию от со. ВЧХ, удовлетворяющая этому требованию, изображена на рнс. 4.4 Кривой 2. ; 3. Если ВЧХ имеет максимум Ра шах (со) (рис. 4.4, кривая 3), то перерегулирование (%) а<-Ш)-10°- 4.Если ВЧХ имеет интервал положительности соп, то при е = 5 % в общем случае время регулирования tp > я/со„. Для монотонных процессов tp > 4л/е»п. 5.Если увеличить (уменьшить) масштаб ВЧХ вдоль оси абсцисс в я раз, то масштаб кривой переходного процесса вдоль той же оси уменьшится (увеличится) в то же число раз. Это свойство иллюстрируется на рис. 4.5, где изображены ВЧХ Р3> (со) и в два раза более «широкая» ВЧХ P8j (со), а также соответствующие им кривые переходного процесса рх (f) и р2 №• Из рисунка видно, что переходный процесс р2 (f) заканчивается в два раза быстрее, чем р, (f). 6.Если изменить масштаб ВЧХ вдоль оси ординат в п раз, то н масштаб кривой переходного процесса р (/) изменится во столько же раз. 7.Конечное значение переходной функции равно начальному значению ВЧХ, т. е. Km Р(г) = Рз(0) (Рис- 4.6). Это положение вытекает из теоремы о конечном 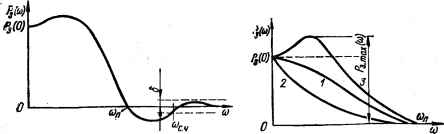 Рис. 4.3. Вещественная частотная харак-Рис. 4.4. Вещественные частотные теристика системы (возможный вид)характеристики САУ. 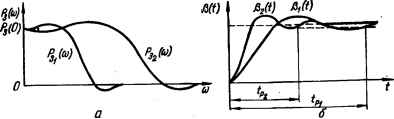 Рис. 4.5. ВЧХ (с) и соответствующие им переходные функции (б). 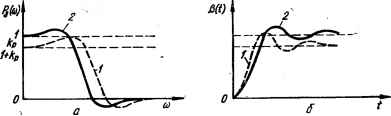 Рис. 4.6. ВЧХ (а) и соответствующие им переходные функции статической (1) и астатической (2) систем (б). значении функции: lim Р (/) = lim рР (р). Учитывая, что при единичном ступвнча» том воздействии р (р) = К3 (р) L [1 (/)] •= К3 (Р)/Р, получаем lim Р (1) =« Р (оо) —> /-> ос = lim рКв (Р)/Р = Hm/f3 (р), или, заменяя р через /со: Р (оо) = lim К3 (/со). р-+0р-»0«0-+С Так как lim К3 (/со) = lim [Р3 (со) + /Оз (ю)] и Сз (и) содержит со в качестве мно-жителя, а следовательно, при со = 0 обращается в нуль, то Hm К3 (/to) — = lim Я3 (со), т. е. Р (оо) = Р3 (0). Значения Р3 (0) и р (оо) для статической и астатической систем соответственно равны р (оо) = Р3 (0) = у(1 + kp) и Р (оо) = Ра (0) = 1. 8. Начальное значение переходной функции р (0) равно -конечному значению Р3 (со) ВЧХ, т. е. lim Р (f) = lim Р3 (со). Это положение вытекает из теоремы о иа-t-+0га-юо чальном значении функции. Во всех случаях, когда порядок числителя Кр (/») меньше порядка знаменателя, Р3 (оо) = 0, а следовательно, переходный процесс начинается из точки, соответствующей началу координат (см. рис. 4.6), На основании рассмотренных простых признаков можно грубо оценить качество переходного процесса в замкнутой САУ по виду ВЧХ. Приближенный метод построения переходной функции с помощью вещественных трапецеидальных частотных характеристик В основе метода косвенного анализа лежит приведенное выше вы- 00 ражение р (f) — (2/я) [Ра (со)/со] sin co/dco, связывающее вещественную о частотную характеристику системы Ра (со) в ев переходной функцией 0 ... 34 35 36 37 38 39 40 ... 143 |












