Раздел: Документация

0 ... 36 37 38 39 40 41 42 ... 143

% может быть любым в пределах от 0 до 1. Переходная функция h (/), соответствующая единичной трапецеидальной характеристике, называется /t-функцией. Значения /t-функций для различных коэффициентов х трапеции сведены в табл. 4.1.

Для построения кривой переходного процесса р\ (/), соответствующего i-й прямоугольной трапецеидальной характеристике с начальной ординатой Рв (0)t-, частотой положительности ип; и коэффициентом наклона %£, необходимо: 1) из таблицы выписать данные для Л-функции, соответствующей единичной трапецеидальной характеристике с коэффициентом наклона Xt; 2) согласно свойствам (пп.5, 6) каждый из интервалов времени *таб, определенный по таблице /t-функций, разделить на а каждую ординату Л-функции умножить на Р3 (0),-.

Пересчет масштабов по осям абсцисс и ординатам удобнее всего выполнить, записывая данные в таблицу следующего вида:

таб	h	Ц = таб/п/	рч т = л/>„<0),

Для получения переходной функции системы 6 (/) на общем графике строятся кривые 3t- (t) переходных процессов, соответствующих всем прямоугольным трапециям, на которые была разбита вещественная частотная характеристика системы, и суммируются ординаты всех кривых. Кривые В (t) строятся с учетом знака начальных ординат Р3(0)г.

Пример 2. Построить переходную функцию следящей системы, ВЧХ которой имеет вид, изображенный на рис. 4.9, а.

Замейяем кривую ВЧХ ломаной абегде н в соответствии с последней разбиваем ВЧХ на четыре прямоугольные трапеции (рис. 4.9, б). Для каждой трапеции из рисунка определяем параметры.

Трапеция 1:

/МО)! =1,58; соа, = 1,2 1/с; соп1 = 2,18 1/с; %t = сой1/соп1 = 0,55. Л Трапеция 2:

Р3(0)2 = —0,16; соо2 = 3,5 1/с; №„2 = 4,66 1/с; \ = соа2/соп2 = 0,75.

Таблица 4.2. Данные для построения переходной функции, соответствующей прямоугольной трапеции 1

Трапеция 1	/>„<0), = 1,58			соп1 =2,18 1/с				X, = 0.55
таб	0,5	1,0	2,0	3,5	6,0	8,0	10,5	15,5	20	25
h	0,248	0,476	0,856	1,152	1,001	0,949	1,002	1,007	0,993	1,002
к = Wwni	0,23	0,46	0,92	1,6	2,75	3,67	4,8	7,1	9,2	11,5
Р, (0 =	0,39	0,75	1,35	1,82	1,58	1,5	1,58	1,59	1,56	1,58
= hp3 (О),

---

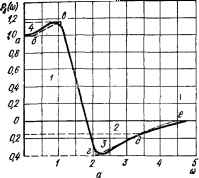1.4 1.2 W 0,8 0,6 0.4 0,2 О -0.2 -OA

	\
	\
	\
	\
1	\
	\
	\	i
		\
	2	;--т

5 а)

Рис. 4.9. К построению переходной функции следящей системы:

a — ВЧХ системы; б — разложение БЧХ на прямоугольные трапецеидальные характеристики.

Рис. 4.10. Переходная функция следящей системы и ее составляющие.

Трапеция 3: з(0)з = -0,24:3 = соп3 = 3,7 1/с; %а-.

Трапеция 4: Рв (0)4 = - 0,18; соа4= 0,24 1/с;

= 2,6 1/с;

:0,7.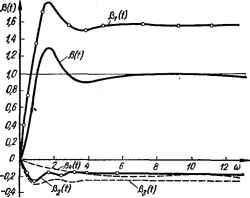

wn4 = 0,8 1/с; Х4 = 0,3.

Из табл. 4.1 выписываем в табл. 4.2 данные для Л-функции единичной трапецеидальной характеристики с коэффициентом

наклона X, равным коэффициенту наклона первой трапеции (Хх = 0,55). Данные пересчета масштабов по осям абсцисс и ординат также записываем в эту таблицу. По данным табл. 4.2 строим кривую Р, (f) (рис. 4.10). Аналогичным образом записываются в таблицы данные для трапеций 2—4 и строятся соответствующие кривые Рг М — 04 М- Просуммировав ординаты всех кривых с учетом знаков ординат, получим результирующую кривую Р (f) переходного процесса системы.

Построение вещественной частотной характеристики замкнутой системы

ВЧХ замкнутой системы может быть построена на основании выражения для Рв (со), которое находится разложением /(3 (/со) на вещественную и мнимую части: К3 (/t°) = (ю) + iQs

Если же в нашем распоряжении имеются ЛЧХ разомкнутой системы, то ВЧХ замкнутой системы проще построить по этим характеристикам с помощью номограммы (рис. 4.11) [64]. Исходным при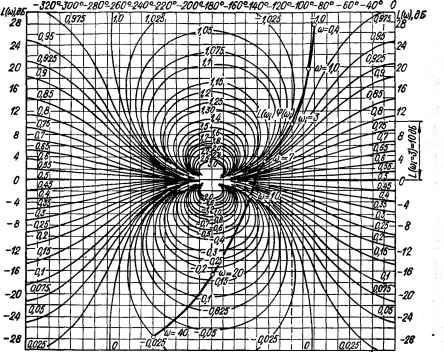

---

-3203(Ю°-Ж-2в0о-240о-220г00е-Г80Ч60-140Ч20-100о-80о-60-40о Ф)

ч>(и; з)=-т°

Рис, 4.11. Номограмма для определения ВЧХ по логарифмическим частотным характеристикам разомкнутой системы.

построении номограммы является выражение Ks(ja>) = Kp(Jg>)/[1 + + КрПодставляя в это выражение /С3 (/<о) = Ps (со) -J- jQs (со) и

/Ср (/со) = N (со) ef,№>), получаем />3 (со) + /Q3 (со) = N (со) eVfl + + 7V(co)e/*(<e>], откуда видно, что ординаты />3(со) ВЧХ замкнутой системы связаны с координатами N (со) и яр (со) частотной характеристики разомкнутой системы. Одному и тому же значению Р3 соответствуют различные координаты N (со) и яр (со). Геометрическое место точек на плоскости, где по оси ординат откладываются значения L (со) = == 20 Ig N (со), а по оси абсцисс — значения яр (со), соответствующие постоянному значению ординаты ВЧХ Рэ, представляет собой определенную кривую. Семейство таких кривых, соответствующих различным значениям Р3, образуют номограмму, с помощью которой можно определить ВЧХ замкнутой системы по ее логарифмическим частотным характеристикам в разомкнутом состоянии.

Для определения ВЧХ замкнутой системы предварительно на номограмме в координатных осях L (со), яр (со) строят логарифмическую амплитудно-фазовую частотную характеристику (ЛАФЧХ) разомкнутой системы на основании известных логарифмической амплитудной

0 ... 36 37 38 39 40 41 42 ... 143