Раздел: Документация
0 ... 37 38 39 40 41 42 43 ... 143 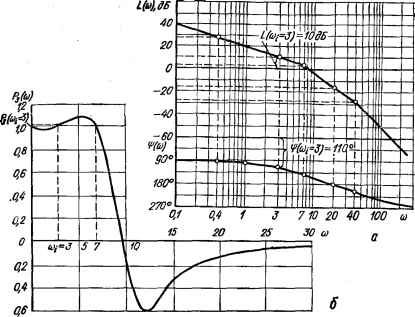 Рис. 4.12. К построению ВЧХ замкнутой системы по ЛЧХ разомкнутой системы: а — ЛЧХ! б — ВЧХ. и фазочастотной характеристик разомкнутой системы. Пусть, например, требуется построить ЛАФЧХ системы по ЛАЧХ и ЛФЧХ, изображенным на рис. 4.12, а. Для построения точки логарифмической АФЧХ, соответствующей какой-либо частоте со£, из ЛАЧХ определяется значение L (щ) = 20 lg N (со,), а из ЛФЧХ — значение тэ (cof) при этой частоте. Например, на частоте щ = 3 L (со,) = 10 дБ, ■ф (cof) = —110°. Найденные значения L (со£) и ф (со£) откладываются соответственно по оси ординат и оси абсцисс плоскости номограммы (рис. 4.11). Точка с координатами L (со,-), ф (со,) и будет являться искомой точкой логарифмической АФЧХ на частоте со,. На рисунке частота со,- указывается при построенной точке. Аналогично определяются другие точки и затем через них проводится кривая — логарифмическая АФЧХ разомкнутой системы. Построенная ЛАФЧХ пересекает кривые Ръ = const. Значения индексов пересекаемых кривых Ps являются значениями ординат ВЧХ замкнутой системы Р3 (со) при частотах, соответствующих точкам пересечения. Выписывая эти значения Р3 с номограммы и откладывая их по оси ординат Р3 (со) при соответствующих частотах, получаем ВЧХ замкнутой системы (рис. 4.12, б). 4.4. Интегральные оценки качества переходного процесса САУ Если переходный процесс системы имеет монотонный затухающий характер (рис. 4.13, а), то переходная составляющая 0П (/) ошибки системы 0 (t) не изменяет своего знака (рис. 4.13, б) и стремится к нулю при t -*~ со. В этом случае для косвенной оценки качества системы может служить интеграл оо /1 = $еп(ол,(4.П) о называемый линейной интегральной оценкой качества. Очевидно, чем меньше интеграл (4.11), тем лучше качество переходного процесса. Интеграл /х может быть легко вычислен. Изображение по Лапласу ошибки оо е„(р)- Je-*en(Q£tf.(4.12) о Из выражений (4.11) и (4.12) следует, что оо h= Je„(Qtf= {6„ (/>)}„=„,(4.13) о т. е. для определения интеграла 1г нужно вычислить лишь изображение по Лапласу ошибки при р = 0, не решая дифференциального уравнения. Если кривая переходного процесса имеет перерегулирование (рис. 4.13, в), когда ошибка изменяет свой знак (рис. 4.13, г), то с помощью линейной интегральной оценки нельзя судить о качестве системы. Действительно, интеграл /х может быть близок к нулю, когда система имеет слабозатухающий колебательный переходный процесс и практически непригодна к работе. Для косвенной оценки качества переходного процесса системы при колебательном переходном процес- 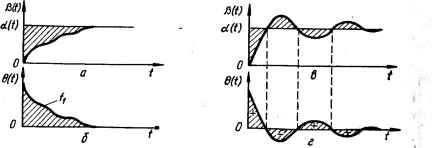 Рис. 4.13. Переходные процессы системы и соответствующие изменения еп (0: а — монотонный; б — изменение 6П (/); в — колебательный; г «*. изменение gn (/). се применяют квадратичные интегральные оценки, не зависящие от знаков ошибки. Интеграл со /.= J [в„(4.14) о является квадратичной интегральной оценкой. Он пригоден для оценки качества как апериодических, так и колебательных процессов. Интеграл /2 также можно вычислять, не решая дифференциального уравнения системы. Как известно, изображение по Лапласу ошибки системы 0 (р) = Кв (р) а (р). Изображение переходной составляющей ошибки 0П (/) = /Се (р) а (р) — 0В (р), где 0В (р) —изображение вынужденной составляющей ошибки. Если порядок астатизма системы v больше порядка высшей производной г задающего воздействия (v > >. г), то в соответствии с формулой (2.73) 0В (/) = 0 и тогда Qn(p) = Ke(p)a(p).(4.15) Поскольку 0П (г) = 0 при t -*- со и t < 0, то для 0П (/) существует изображение Фурье (частотный спектр), определяемое формулой со еп(/со) = Je„(0e-/erf£ff.(4.16) о Сравнивая выражения (4.16) и (4.12), замечаем, что en(/co) = {0n(p)}p==/ffl,(4.17) т. е. 0П (/со) можно найти путем подстановки р = /со в изображение ошибки по Лапласу (4.15). Функцию ошибки 0П if) можно представить в виде интеграла Фурье оо e"W = -2lT J 0п(/)Лсо.(4.18) Исходя из равенства (4.18), можно записать оооооо j [0П (О]2 dt = JL \ 0П (0 dt \ 0П (/со) Лео = О0—оо оооо = - 2F I е" (/«>) $ 0п (0 е7".(4.19) —ооО оо Учитывая, что J 0П (г) е/ис# есть величина, сопряженная с 0„(/со) о оо (см. (4.16)), т. е. j 0Г (t)eatdt = 0П (/со), выражение (4.19) можно пере- о писать в виде j [в„ (012 Л = JL J 0П (/со) 0П (/со) dco, О—оо 0 ... 37 38 39 40 41 42 43 ... 143 |












