Раздел: Документация
0 ... 31 32 33 34 35 36 37 ... 143
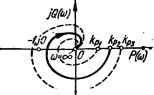 д~ Рис. 3.10. К определению запаса устойчивости по модулю: р — АФЧХ устойчивой системы; б — изменение АФЧХ и запаса устойчивости О системы с изменением Обычно для нормальной работы требуется, чтобы а = 10... 15 дБ. При таком запасе устойчивости изменения параметров системы, как правило, не приводят к потере ее устойчивости. Модуль КПФ N (со), как было показано выше, пропорционален коэффициенту усиления разомкнутой системы kp: N (со) = kp VPo(co) + Q0(co), а ее аргумент яр (со) = arctg [Q0 (со)/Р0 (со)] не зависит от kp. Поэтому АФЧХ системы при увеличении kp, не изменяя своей формы, пропорционально расширяется, а при уменьшении kp сжимается, как показано на рис. 3.10, б. Это значит, что при увеличении kp АФЧХ может измениться так, что будет охватывать критическую точку (—1, /О), т. е. система может перейти в неустойчивый режим. Для характеристики степени устойчивости недостаточно знать только запас устойчивости по модулю. Например, возможен случай, что АФЧХ (рис. 3.11) пересекает вещественную ось далеко от критической точки, а следовательно, система имеет большой запас устойчивости по модулю о, но затем АФЧХ проходит близко к этой точке. Последнее свидетельствует о малой степени устойчивости системы. Для более полной характеристики устойчивости системы введено понятие запаса устойчивости по фазе. Для выяснения запаса устойчивости по фазе системы, имеющей АФЧХ 1, показанную на рис. 3.12, проведем окружность единичного радиуса с центром в начале координат. Частота в точке ее пересечения с АФЧХ 1 называется частотой среза сос. Проведем вектор Кр (/сос) в эту точку. Модуль N (сос) = 1, т. е. на частоте сос выполняется условие самовозбуждения системы по амплитуде. Изменим АФЧХ так, чтобы система перешла к границе устойчивости (АФЧХ 2). При этом вектор К (/«с) единичной длины повернется по часовой стрелке на угол у до совпадения с отрицательной вещественной осью и аргумент КПФ яр (сос) = яр (со„) ж= —180°, т. е. будет выполняться условие самовозбуждения по фазе. Угол у между вектором КПФ, модуль которого равен единице, и отрицательной вещественной осью называется запасом устойчивости по фазе. Таким образом, запас устойчивости по фазе характеризует отличие фазового угла яр (сос) АФХ разомкнутой системы на частоте среза от  Рис. 3.11. АФЧХ системы, име-Рис. 3.12. К определению ющей достаточный запас устой-запаса устойчивости по чивости по модулю, но малуюфазе, степень устойчивости. критического значения угла яр (со„) = —180°, при котором удовлетворяется фазовое- условие самовозбуждения системы. Обычно обеспечивается запас устойчивости по фазе у = 30...45°. При таком значении V возможные изменения параметров системы, как правило, не приводят к потере ее устойчивости. Для определения того, устойчива система или нет, не обязательно строить всю АФЧХ, а достаточно найти точку пересечения АФЧХ с вещественной осью. Для этого необходимо из уравнения Q (со) = 0 определить частоту, при которой АФЧХ пересекает вещественную ось, и подставить ее в выражение для Р (со) (здесь Q (со) и Р(со) — мнимая и вещественная частотные характеристики разомкнутой системы). Логарифмический частотный критерий устойчивости Построение АФЧХ сложных систем с целью исследования их устойчивости требует большой затраты времени. Этот процесс существенно упрощается при применении логарифмических частотных характеристик (ЛЧХ). Простота и наглядность метода ЛЧХ объясняются простотой построения логарифмических частотных характеристик и очевидной связью параметров системы с видом этих характеристик. Применение метода ЛЧХ дает возможность наглядно видеть влияние того или иного параметра системы на ее устойчивость и переходный процесс, а также позволяет сравнительно просто определить характеристику корректирующего устройства, обеспечивающего требуемые показатели качества системы. Логарифмический частотный критерий устойчивости основывается на амплитудно-фазовом критерии устойчивости и представляет по существу более удобную его формулировку. Рассмотрим только случай, когда САУв разомкнутом состоянии устойчива. Вначале выясним критерий устойчивости для САУ первого рода, имеющих наиболее простые по своей форме частотные характеристики. На рис. 3.13, а изображены АФЧХ разомкнутых систем, отличающихся лишь коэффициентами усиления k\ (&р2 > kv\). Из них АФЧХ 1, : согласно амплитудно-фазовому критерию устойчивости, соответствует устойчивой, АФЧХ 2 — неустойчивой системе в замкнутом состоянии. 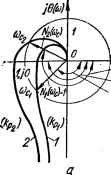 ЩШ Р(и) 180° Цш\дБ О *% -90" -180° -270° 4Ы Л,) С!
Рис. 3.13. Частотные х-чктеристик" систем, отличающихся коэффициентом усиления: с — АФЧХ; б — лчх. На рис. 3.13, б приведены ЛЧХ, соответствующие АФЧХ, изображенным на рис. 3.13, а. Поскольку системы отличаются лишь коэффициентом усиления &р,то их ЛФЧХ совпадают, а ЛАЧХ 2 системы с kp2 располагается выше, чем ЛАЧХ 1 системы скр\. Из рис. 3.13, а следует, что устойчивость системы обеспечивается, если аргумент яр (сос) комплексной передаточной функции системы при частоте среза сос по абсолютной величине меньше 180°. Применительно к ЛЧХ это условие устойчивости можно сформулировать следующим образом: система автоматического управления, устойчивая в разомкнутом состоянии, будет устойчива и в замкнутом состоянии, если ордината логарифмической фазочастотной характеристики (аргумент комплексной передаточной функции) на частоте среза сос системы по абсолютной величине меньше, чем 180°, т. е. если яр (ос) [< 180°. Система с ЛАЧХ 1 (рис. 3.13, б) устойчива, поскольку ярх (сос) <; < 180°, а система с ЛАЧХ 2 неустойчива, так как яр2 (toc) > 180°. Система находится на границе устойчивости, если ее АФЧХ в разомкнутом состоянии проходит через точку с координатами —1, /0, т. е. если на частоте соя, на которой система вносит запаздывание яр (соя) =—180°, модуль N (соя) КПФ равен 1. Поскольку 20 lg 1 = 0, то система будет находиться на границе устойчивости, если на частоте соя ЛАЧХ будет пересекать ось 0 дБ, т. е. если to0 = со„. ЛЧХ системы, находящейся на границе устойчивости, изображены на рис. 3.14. 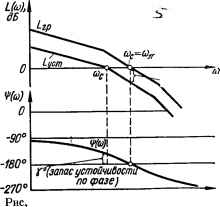 6 (запас устойчи- вости по амплитуде) 3.14. К определению запаса устойчивости по амплитуде и фазе. 0 ... 31 32 33 34 35 36 37 ... 143 |












