Раздел: Документация
0 ... 53 54 55 56 57 58 59 ... 143 1+Tp Хо.с 20lgk 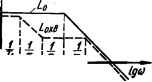 Рис. 5.26. Охват апериодического звеиа гибкой обратной связью, содержащий дифференцирующий контур с передаточной функцией Ка с (р) = xpl(xp -- 1): с — структурная схема; 6 — ЛАЧХ при отрицательной обратной связи н при т > Т. вводить дифференцирующие звенья, передаточные функции которых содержали бы в качестве сомножителя /со. При этом нужно иметь в виду, что если обратной связью охватываются интегрирующие звенья, передаточные функции которых содержат /со в качестве сомножителей в знаменателе, то степень п при /со звена обратной связи должна быть выше степени v при /со знаменателя передаточной функции охватываемых звеньев: n>v.(5.39) В этом случае действительно будет выполняться условие (Б.38): lim К0 (/со) Ко.с (/со) = lim и->0<л-*0 Ко. (М KccAMifaf = 0«1. Чтобы при охвате апериодического звена не уменьшался его коэффициент усиления, достаточно в цепь обратной связи ввести звено, содержащее /со в первой степени. Действительно, в этом случае lim Ко (/со) Ксс (/со) = lim I -. -, Ко.Со (М /со I = О, <о-о<й-»-о \ 1110~г1 т. е. условие (5.37) выполняется и, следовательно, коэффициент усиления звена не уменьшается. Реализовать такую обратную связь можно с помощью дифференцирующего звена. На рис. 5.26, а в цепь обратной связи включено дифференцирующее звено (см. схему 1 табл. 5.1) с передаточной функцией Ко.с (р) = тр/(тр + 1), поэтому на вход апериодического звена подается величина, пропорциональная производной от выходной величины этого звена. В установившемся режиме, когда выходная величина апериодического звена имеет постоянное значение, обратная связь не влияет на работу звена. Передаточная функция звена, эквивалентного апериодическому звену, охваченному гибкой обратной связью, в соответствии с, выражением (5.28) будет иметь вид: ЩТр + 1) я (тр + 1) К0*в (р) = 1± Txp* + (T + x±kt)p + 1 (Тр+ 1)(тр+ 1) или после разложения знаменателя на множители Яохв (р) = k (тр + 1)/[(7\р +1) (72р + 1)], , (Б.40) (5.41) тде 7\ и Т2 находятся из системы уравнений 74 = ТХТ2; T + x±kx = T1 + Т2, полученной приравниванием коэффициентов при одинаковых степенях р знаменателей формул (5.40) и (5.41). При отрицательной обратной связи: 7\,2 = [Т + т + kx ± У(Т + х + kxf — 47т]/2. (5.43) Как видно из выражения (5.41), эквивалентная схема представляется двумя апериодическими и одним дифференцирующим звеньями, соединенными последовательно. Постоянные времени этих звеньев зависят от вида (положительной или отрицательной) обратной связи и по-•стоянной времени т (см. формулу (5.43)) дифференцирующего контура в обратной цепи. Благодаря этому возникают широкие возможности изменения частогных характеристик эквивалентного звена в желаемом направлении. Коэффициент усиления эквивалентной схемы в данном случае не изменяется относительно коэффициента усиления апериодического звена, поскольку выполняется условие (5.39): л = 1, v = 0, n>v. В качестве примера определим, как изменяется ЛАЧХ апериодического звена в случае его охвата гибкой отрицательной обратной связью, содержащей дифференцирующий контур и постоянная времени которой т > Т. В соответствии с выражением (5.42) 7\ > т >. > Т> Т2. На рис. 5.26, б показаны ЛАЧХ апериодического звена L0 (со), эквивалентного звена LOXB (со) и ЛАЧХ Ln (со), равная разности LOXB( со) hL„ (со). Из рисунка видно, что охват апериодического звена гибкой отрицательной обратной связью с дифференцирующим контуром при т > Т равносилен включению последовательно апериодическому звену интегро-дифференцирующего контура с передаточной функцией Кп (р) = (тр + 1) (Тр + l)/[{TlP + 1) (Т2р + 1)], (5.44) где Тг и Т2 определяются выражением (5.43); Т равна постоянной •времени апериодического звена, а т — постоянной времени дифференцирующего контура. Охват обратной связью интегрирующего звена Охват интегрирующего звена жесткой обратной связью. Передаточ- ■ ная функция /Сохв(р) звена, эквивалентного интегрирующему звену <с жесткой отрицательной обратной связью (рис. 5.27, а): ■где охв — kjkotck\ охв == f/o.c» (5.42)
M r-»4 xo.c 66 Рис. 5.27. Охват интегрирующего звена обратной связью: а жесткой; б — по первой производной; в — по второй производной. т. е. охват жесткой отрицательной обратной связью интегрирующего звена превращает последнее в апериодическое звено, что может привести к понижению порядка астатизма системы. Охват гибкой обратной связью интегрирующего звена. Условие сохранения порядка астатизма системы. Как только что установили, при охвяте жесткой обратной связью интегрирующего звена получаем эквивалентное апериодическое звено, т. е. понижается порядок астатизма системы. Это не всегда желательно. Чтобы не уменьшался порядок астатизма системы, знаменатели передаточной функции /Сохв (р) эквивалентной схемы и передаточной функции К0 (р) охватываемых обратной связью звеньев должны иметь в качестве общего множителя оператор р в одной и той же степени. Выясним, при выполнении каких условий это требование удовлетворяется. Перепишем выражение (5.28) в явном виде относительно р: Кохв (р) * оп (Р) 1 ± [К0о (p)/Pv] К0.с, (р)рп pv 11 ± К0о (р) К0.с. (р) p"/pv] где lim Ко0 (Р) ф 0, lira /Со.с0 (р) ФО, v — число охваченных связью Р-+0p-s-0 интегрирующих звеньев; п—порядок производной на выходе обратной связи. Если п v, то Аохв(р) = PV[1 ±tfo>>*o.c»P"~Vj т. е. если порядок производной на выходе обратной связи равен числу охваченных обратной связью интегрирующих звеньев или выше его, то порядок астатизма системы не изменяется. Если n<v, то к (п) ==ЧСр> OXBV" Pvll±K0o(P)Ko.C0(p)/pv-n] Pn[Pv-n±K0a(P)Ko.c,(p)\ т. е. порядок астатизма уменьшается и становится равным порядку производной, вырабатываемой дифференцирующим устройством в цепи обратной связи. Таким образом, чтобы при охвате обратной связи интегрирующих звеньев не понижался порядок астатизма системы, необходимо выпол- 0 ... 53 54 55 56 57 58 59 ... 143 |












