Раздел: Документация
0 ... 55 56 57 58 59 60 61 ... 143 эс *1 -И ьоо Vox \Ко.с(Р) к- Рис. 5.29. Структурная схема системы, скорректированной с помощью обратной связи. на сложением ординат ЛАЧХ LH.CK (со) нескорректированной системы и ЛАЧХ Ln (со) эквивалентного последовательного звена. Построение-ЛАЧХ LH.CK (со) не вызывает затруднений. Поскольку выражение для К„ (/со) содержит сумму в знаменателе, то построение ЛАЧХ Ln (со) затруднено, поэтому ее строят по областям частот. В областях частот, в которых /*Со/го)Со.с(/со) I, или Ко.ос (/со) I = l ИК0 (/со)/С0.с (/со) 15> 1, или в логарифмическом масштабе Z.o.oc (to) = — L0 (со) — L0.c (со) > 0, выражение (5.53) принимает вид. Кп (/со) = 1 или Ln (со) = 0, т. е. в областях частот, в которых вспомогательная ЛАЧХ Lo.cc (со) > 0, ЛАЧХ Ln (со) совпадает с осью 0 дБ. В областях частот, в которых К0 (/со) Ко. (/со) > 1, или Ко.ос (/со) = \1К0 (/со) Ко.с (/со) < 1, или в логарифмическом мае штабе Lo.oc (со) = — LD (со) — L0.c (со) < 0, выражение (5.53) примет вид К„ (/со) = {/Ко (/со) /Сох (/со), т. е. в областях частот, в которых £о.ос(со)<0, ЛАЧХ £п(со) совпадает с ЛАЧХ L0.oC(co). Построив ЛАЧХ нескорректированной системы LH.CK (со) и сложив ее с ЛАЧХ L„ (со), получаем ЛАЧХ скорректированной системы LCK (со). Пример 1. Построить ЛАЧХ следящей системы (рис. 5.30, а), скорректированной охватом гибкой отрицательной обратной связью по второй производной двух апериодических и одного интегрирующего звеньев. Удобно принять следующую методику построения 1.Определяем КПФ нескорректированной системы «"и.ск W = *н (М Ко (/<*) = V№ + 0 № + ) (ri/m + 1) /©, где kp = kgkki; Т\> Т2> Ts, и в соответствии с этим выражением строим ЛАЧХ LK ск (со) нескорректированной системы (рис. 5.30, б). 2.Определяем *о.ос(/ш): о (/ш) К0 с (/со) fКМУсо +1) /со (7\/со +1)] /гхгт (/со)2/(т/со +1) где йоос= \lkxk2kTVi, и строим ЛАЧХ ос (со) в соответствии с этим выражением (рнс. 5.30, б). Отмечаем частоты пересечения L0 ос (со) с осью 0 дБ <% и а>2, которые являются частотами сопряжения ЛАЧХ Ln (со). 3. Стронм ЛАЧХ L„ (со). В областях частот со < со, н <о> со2, где Looc (ю) > 0, Ln (со) совпадает с осью 0 дБ (рис. 5.30, б, отрезки аб н еж). В области же частот сог < < со < соа, где Z.aoc (со) < 0, Ln (со) совпадает с ЛАЧХ Looc (со) (рис. 5.30, б, ломаная бвгде). Полная ЛАЧХ Ln (со) на рис. 5.30, б изображена пунктирной ломаной. Усилитель-UruniimfiiH, ЭС преобразователь Усилитель Двигатель JB 1/о.с ЪР+1 к, Ър+1 X р Wfi} KoJp) rp+1 Диек%нтуртий Tax<**»ePm°P Ць>),дБ  Рнс. 5.30. К примеру построения ЛЧХ следящей системы, скорректированной обратной связью: а — структурная схема системы; б — построение ЛЧХ системы. 4.Сложением L„ ск (со) и Ln (со) получаем ЛАЧХ скорректированной системы 5.Из построенной ЛАЧХ lck (со) скорректированной системы определяем ее передаточную функцию VckWH" 1) *р.ск №») (Г1к/и + 1} (г2к/(0 + 1)а (7уи + 1} /ш • (5.54) где постоянные времени TlK — 1/cOj и Т2к = 1/соа находятся из ЛАЧХ системы, kp ск = — kp = kykk. 6. В соответствии с выражением (5.54) для /*Ср ск (/со) записываем формулу для ФЧХ скорректированной системы: фск (со) == — 90° — arctg соГ1к + arctg сот —- 2 arctg соГ—arc tg со7\, и по ней стронм ее ЛФЧХ фск (со). Для сравнения на рис. 5.30, б кривой ф (со) изображена ЛФЧХ нескорректированной системы. Из сравнения ЛЧХ исходной и скорректированной системы видно, что введение местной отрицательной обратной связи делает систему устойчивой с необходимым запасом устойчивости. Как видно из рис. 5.30, б, охват гибкой обратной связью по второй производной двух апериодических и интегрирующего звеньев равносильно последовательному включению в систему контура интегро-дифференцирующего типа, -f-o 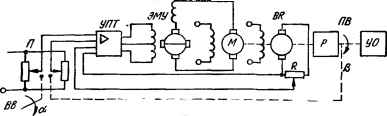 Рис. 5.31. Схема следящей системы, скорректированной с помощью тахо-метрической обратной связи по первой производной. • *Гп(/со) = - ЛАЧХ которого имеет вид, изображенный ломаной Ln (со), а передаточная функция определяется выражением (t/a+lHrjco+lHTJco+l) (Г1к/со+ 1)(Г2к/со+1)3 • Из рис. 5.30 видно, что ЛАЧХ L№ (со) на частоте со2 изменяет наклон на —40 дБ/дек, что свидетельствует о возможности возникновения в системе колебательного звена. Точная ЛАЧХ колебательного звена отличается от приближенной наличием «пика» (см. рис. 2.23, а). Такой же пик может иметь и точная ЛАЧХ Z.CK (со) в области со2 и поэтому не исключена возможность, что LCK (со) в этой области частот еще раз пересечет ось 0 дБ. Если на новой частоте среза сос2 ф (со) >180°, то система окажется неустойчивой. Поэтому в этих случаях следует провести дополнительные исследования устойчивости или выбором параметров обратной связи и коэффициента усиления Яр системы стремиться к тому, чтобы L„ (со), а следовательно, (со) не имела изменений наклона больше чем 20 дБ/дек. Примеры схемного осуществления коррекции САУ с помощью обратных связей. Элементы и схемы получения напряжения, пропорционального частоте вращения исполнительного двигателя. На рис. 5.31 изображена схема следящей системы с элект-ромашннным усилителем мощности, скорректированной с помощью тахометрической обратной связи (обратной связи по первой производной). С валом исполнительного двигателя М непосредственно или через редуктор Р соединяется тахогенератор постоянного тока BR. Последний представляет собой малогабаритный генератор с независимым возбуждением или с постоянными магнитами. Напряжение тахогенератора, снимаемое со щеток якоря, пропорционально скорости вращения двигателя (производной от угла поворота приемного вала). Полярность напряжения тахогенератора, зависит от направления его вращения. Напряжение тахогенератора с обратным знаком подается на вход усилителя постоянного тока УПТ. Коэффициент обратной связи регулируется потенциометром R. Этот пример соответствует коррекции системы путем охвата трех апериодических" н интегрирующего звеньев обратной связью по первой производной (обычно электромашинный усилитель представляется двумя апериодическими, а двигатель —• апериодическим и интегрирующим звеньями). Рассмотрим физический смысл введения обратной связи по первой производной. Предположим, что при изменении скачком скорости вращения ведущего вала ВВ (на рис. 5.32, а для этого случая прямой а изображено изменение угла а ведущего вала, а на рис. 5.32, б прямой kda/dt — изменение частоты вращения этого вала), управляемая величина системы Р (угол поворота приемного вала ПВ) в режиме переходного процесса изменяется по кривой Р (рис. 5.32, а). На рис. 5.32, б кривой kdQIdt изображена величина, пропорциональная первой производной от управляемой величины системы. Первую производную kdfi/dt можно разложить на постоянную ыр/йг=*(рис. 5.32, в) и переменную kdfildt составляющие. Рассмотрим, какое воздействие на работу системы оказывают переменная и постоянная составляющие этой производной. Составляющая kd$/dt возникает в режиме переходного процесса и, естественно, влияет на работу системы лишь в переходном режиме, изменяя переходную функцию системы. Напряжение обратной связи на входе 0 ... 55 56 57 58 59 60 61 ... 143 |












