Раздел: Документация
0 ... 59 60 61 62 63 64 65 ... 143 Возможность достижения инвариантности в комбинированных системах согласуется с критерием реализуемости инвариантности Петрова [53, 54] — принципом двухканальности. Для достижения полной компенсации возмущающего воздействия необходимо, чтобы компенсационный канал был идентичен каналу возмущения управляемого объекта. Этот вывод подтверждается проведенным здесь анализом. Действительно, из формулы (6.11) следует: K»ls(p)K2(p) = Kl(p). т. е. абсолютная инвариантность системы (рис. 6.1) будет достигнута, если передаточная функция компенсационного канала K.bls (р) К2 (р) будет равна передаточной функции канала возмущения Kl (р). Учет условия физической реализуемости связи по возмущению. В комбинированных системах нет противоречия между условиями инвариантности и устойчивости и благодаря этому в них возможно достижение высокой точности управления. Однако при конструировании инвариантных систем возникают трудности другого характера, связанные с тем, что на передаточную функцию Kbl (р) второго канала накладываются ограничения, определяемые условиями физической реализуемости. Передаточная функция связи по возмущению Kbl (р) в общем случае может быть записана в виде к , (гч - У" + tiP"~ + ■ • • + т„ d*l <Р)Г613. Условие физической реализуемости этой передаточной функции имеет вид пт,(6.14) т. е. степень числителя физически реализуемой передаточной функции меньше степени его знаменателя или равна ей. Если передаточная функция связи по возмущению Kbl (р), найденная в соответствии с формулой (6.11), отвечает условию физической реализуемости (6.14), то в системе возможно достижение абсолютной инвариантности ошибки относительно возмущающего воздействия L (.). В том случае, когда ■Кв/.. (р) оказывается физически нереализуемой, полная компенсация влияния возмущающего воздействия L (.) невозможна. Пример 1. Дана САУ (рнс. 6.1), имеющая передаточные функции: *itP>= /t-.-i-i.it. „ i.li : *-M= /т-nlnn ; KLiP) (7>+1)(Г2кр+1) "X2U" (Tzp+Dp(TLp+l)p- Найти передаточную функцию Kbl (p) связи по возмущению, прн которой обеспечивается абсолютная инвариантность ошибки системы относительно возмущающего воздействия. В соответствии с формулой (6.11) * .</» kBL(T2p+\) IkL Ч (p} = W " tlp + i • I = -hV) <6Л5> т. е. передаточная функция KbL (р) физически реализуема и связь может быть осу- а ществлена с помощью корректирующего устройства, имеющего передаточную функцию (6.15). 6.3. Условие абсолютной инвариантности ошибки относительно задающего воздействия и возможность его реализации в комбинированных следящих системах В следящих системах основной причиной, вызывающей ошибку воспроизведения 6 (7), является изменение задающего воздействия a (t). С целью упрощения исследования связи между Q (t) и a (t) примем L (t) = 0. Тогда уравнение (6.1) системы для ошибки будет иметь вид F(p)Qa(t) = M{p)oL(p).(6.16) Из этого уравнения видно, что если будет выполняться условие М(р) = 0,(6.17) то ошибка Qa (t) = 0 при любом законе изменения a (t). Условие (6.17) является условием абсолютной инвариантности ошибки следящей системы относительно задающего воздействия. В одноконтурных системах с принципом управления по отклонению, как показано в первой главе, абсолютная инвариантность ошибки 8а (г) относительно задающего воздействия недостижима. Исследуем возможность выполнения условия абсолютной инвариантности (6.17) в комбинированных следящих системах. Комбинированная следящая система (см. рис. 1.11, б) отличается наличием связи СЗВ по задающему воздействию a (t). Передаточная функция этой связи на структурной схеме системы (рис. 6.2) обозначена Ква (р)- В соответствии со схемой уравнения элементов системы имеют вид: е«(р) = а(р)-Р(р);(6.18) 2 (Р) = Кг (р) 6« (р) + Кю (р)а (р);(6.19) Р(р)=*.(Р)2(р).(6.20) Исключив из этих уравнений В (р) и 2 (р), получим уравнение системы для ошибки [1 + Кг (р) К* (р)] 6а (р) = [1 - К2 (р) Ква (р)] а (р) (6.21) или после подстановки значений Ki (р) = D,- {p)IFt (р) (i = 1, 2, в а) [Рг (Р) F2 (р) + Dx (р) D2 (р)] FBK (р) еа (р) = = [F2 (р) FBa (р) - D2 (р) Dm (р)] F1 (р)а (р).(6.22) 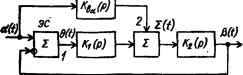 Рис. 6.2. Структурная схема комбинированной следящей системы со связью но задающему воздействию. Условие абсолютной инвариантности 8а (р) относительно а (р): 1-КАр)Кв*а(р) = 0(6.23) или М (р) = [Fa (р) FB« (Р) - Du (р) Dsa (р)] F, (р) = 0. Если учесть, что Ft (р) Ф 0, то условие инвариантности примет вид Fa (Р) Fsa (р) — D2 (р) DBa (р) = 0.(6.24) Поскольку левая часть формулы (6.24) является разностью, то имеется принципиальная возможность выполнения условия инвариантности за счет выбора DBCt (р) и FBCt (р). Передаточная функция связи по задающему воздействию, удовлетворяющая условию абсолютной инвариантности (6.24): (р) = Dta <p)/FBa (р) = F2 (p)/Da (р) = 1 /К* (р). (6.25) Выясним, возможен ли выбор Ква (р) из условия инвариантности е точки зрения устойчивости системы. Из сравнения условия инвариантности (6.24) и характеристического уравнения системы IFi (Р) F2 (р) + А, (р) D2 (р)] /ва (р) = 0(6.26) видно, что полином DBa (р) (числитель функции Ква (р)) входит только в условие инвариантности. Поэтому его выбор из условия инвариантности не влияет на устойчивость системы. Полином Fm (р) (знаменатель функции Ква (р)) входит как в условие инвариантности (6.24), так и в характеристическое уравнение системы (6.26). Из формулы (6.26) видно, что FBa (р) входит в характеристический полином системы в виде сомножителя. Поэтому с введением связи по задающему воздействию корни характеристического уравнения (устойчивость) замкнутой части системы не изменяются, а появляются лишь новые корни, определяемые характеристическим уравнением F (р) = 0. Эти корни определяют устойчивость разомкнутой части комбинированной системы — связи по задающему воздействию. В разомкнутых системах не возникает проблемы устойчивости, поэтому в комбинированной системе выбор полиномов DBa (р) и (р) из условия инвариантности не приводит к потере устойчивости. Отсюда можно сделать вывод, что в комбинированных следящих системах со связью по задающему воздействию нет противоречия между условием инвариантности (8a (t) относительно a (t)) и условием устойчивости. Передаточная функция КваЙ (р) связи по задающему воздействию, при которой ошибка системы инвариантна относительно задающего воздействия, как видно из формулы (6.25), представляет собой выражение, обратное передаточной функции К2 (р)- Степень / числителя передаточной функции К2 (р) участка следящей системы, обычно содержащего интегрирующий элемент (например, электродвигатель), К* (Р) = D2 (pf/F2 (p)(ft) ниже степени ее знаменателя k (/ <; k). У передаточной же функции Ква. (р) — 2 (p)(*/D2 (р)(Л степень числителя k оказывается больше степени знаменателя /, что находится в противоречии с условием физической реализуемости (6.14). Из этого 0 ... 59 60 61 62 63 64 65 ... 143 |












