Раздел: Документация
0 ... 62 63 64 65 66 67 68 ... 143 6.6. Следящие системы с принципом управления по отклонению и дифференциальными связями. Итерационные системы В комбинированных следящих системах, как было показано, возможно достижение высокой точности управления. Из структурной схемы комбинированной следящей системы (рис. 6.2) видно, что для построения последней необходимо измерять задающее воздействие а и через звено Ква (р) подавать на сумматор 2. В тех случаях, когда возможность непосредственного измерения задающего воздействия отсутствует, можно измерять а косвенным способом, оставаясь в рамках системы с принципом управления по отклонению. Для этого используется элемент сравнения, являющийся функционально-необходимым, элементом следящей системы с управлением по отклонению. Действительно, из уравнения элемента сравнения системы (рис. 6.2) 6 (0 = a (t) — В (г) находим a (t) = 6 (/) + В (f), откуда видно, что для получения задающего воздействия достаточно осуществить сложение ошибки системы G (t) и управляемой величины В (t), т. е. сложение сигналов на входе и выходе элемента сравнения. Такой метод косвенного измерения задающего воздействия называется методом дифференциальной связи или методом «вилки». Структурная схема следящей системы с принципом управления по отклонению, в которой осуществляется косвенное измерение задающего воздействия с помощью дифференциальной связи, изображена на рис. 6.4. Следящая система с принципом управления по отклонению (рис. 6.4), в которой измеренное с помощью дифференциальной связи задающее воздействие а через звено с передаточной функцией Ква. (р), совпадающей с передаточной функцией связи по задающему воздействию комбинированной системы (рис. 6.2), подается на сумматор 2, эквивалентна комбинированной следящей системе [18, 20]. В последнее время наряду с комбинированными системами находят широкое применение итерационные САУ [50, 60]. Как известно, управляемая величина 6 (t) системы (см. рис. 2.4) отличается от задающего воздействия a (t) на величину ошибки: G (t) = a (t) — 6 (t). Если к управляемой величине В (t) после точки ответвления главной обратной связи прибавить ошибку 0 (г) (рис. 6.5, а), то управляемая величина на выходе сумматора 1 системы Ви (t) = В (г) + 0 (/). В этом случае ошибка системы 0И {t) = a (t) — Ви (t) = a (t) — В (t) — ЭС * z ВЦ) Т lit) ЛИ/ Рис. 6.4. Структурная схема следящей системы с принципом управления по отклонению и дифференциальной связью. 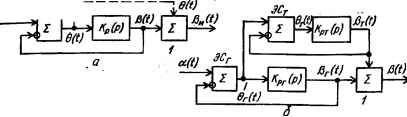 Рис. 6.5. Структурные схемы итерационнг-х систем: а — идеальной; б — двухканалытой. — 6 (0 = 0. Поскольку управляемая величина системы (например, угол поворота антенны) и ошибка системы (электрическое напряжение) имеют различную физическую природу и энергетические параметры, то непосредственно подать ошибку системы с выхода элемента сравнения ЭС на сумматор 1, как показано штриховой линией на рис. 6.5, а, не представляется возможным. Для формирования сигнала -т (.), близкого к ошибке, обычно применяется вторая (точная) следящая система, задающим воздействием которой является ошибка 6Г (.) основной (грубой) следящей системы (рис. 6.5, б): на элемент сравнения ЭСТ точной системы подается ошибка 6Г (.) грубой системы. Выходная величина 6Х (.) точной системы отличается от 6Г (.) на величину ошибки точной системы 6Т (t) = 6Г (t) — В- (t). Поскольку значение 0Т (f) обычно мало, то благодаря применению данной системы, называемой итерационной, удается существенно повысить точность воспроизведения. В случае необходимости дальнейшего повышения точности можно дополнительно ввести не только первую систему, но также вторую, третью и т. д. Значительных результатов повышения точности следящих систем следует ожидать от применения систем, сочетающих структуры итерационных и комбинированных систем. ГЛАВА 7 Статистические методы исследования систем автоматического управления 7.1. Необходимость исследования САУ при случайных воздействиях с помощью статистических методов В предыдущих главах рассматривались вопросы определения точности САУ при детерминированных, т. е. известных, заданных возмущающих и задающих воздействиях. Например, точность системы в переходном режиме оценивалась с помощью показателей качества переходного процесса, являющегося реакцией системы на типовое воздействие в виде единичной ступенчатой функции. Точность системы в установившемся динамическом режиме оценивалась с помощью установившихся динамических ошибок при типовом воздействии, заданном, например, в виде полинома (2.69). Однако часто задающие (возмущающие) воздействия представляют собой случайные, непрерывно изменяющиеся функции времени, аппроксимация которых типовыми функциями времени либо невозможна, либо приводит к существенным погрешностям. В качестве примера можно назвать следящую систему радиолокационной станции, обеспечивающую автоматическое сопровождение цели. В ней задающим воздействием являются координаты движения цели, закон изменения которых заранее не может быть определен. На задающее воздействие системы накладываются помехи или флуктуации, представляющие собой быстроизменяющиеся случайные функции времени. Эти флуктуации входного сигнала, являющиеся возмущающими воздействиями, вызываются непрерывным изменением коэффициента отражения цели, его центра отражения вследствие рыскания, качки цели и другими причинами. Шумы, возникающие в элементах радиолокационных устройств, имеющие случайный характер, также накладываются на полезный сигнал. Возмущающим воздействием системы автоматического сопровождения цели по направлению является ветровая нагрузка на антенну, которая также представляет собой случайную функцию времени. Задающие и возмущающие воздействия, являющиеся непрерывно изменяющимися случайными функциями времени, как отмечалось, не . могут быть заменены типовыми воздействиями, поэтому и рассмотрен-,ные ранее показатели качества не могут быть использованы для оценки поведения системы, к которой приложены такие воздействия. Наиболее правильным подходом к исследованию САУ, находящихся под влиянием случайных воздействий, является подход с позиций теории вероятностей, так как только вероятностные статистические методы дают возможность учесть случайный характер воздействий. Появление и развитие статистических методов анализа и синтеза САУ при наличии : воздействий в виде случайных функций времени не умаляет значения методов анализа и синтеза при воздействиях в виде заданных функций времени, а лишь расширяют возможности в отношении более полного учета реальных условий работы системы. . Статистические методы анализа и синтеза САУ хорошо разработаны , и доведены до инженерных методов расчета для случая стационарных случайных воздействий, охватывающих сравнительно широкий круг воздействий. Для так называемых квазистационарных случайных процессов, отличающихся тем, что характеристики их изменяются во • времени сравнительно медленно, В. С. Пугачевым разработан метод, по структуре мало отличающийся от метода для стационарных слу- , чайных процессов (спектрального метода), но применяемый в более i широком диапазоне условий. 0 ... 62 63 64 65 66 67 68 ... 143 |












