Раздел: Документация
0 ... 61 62 63 64 65 66 67 ... 143 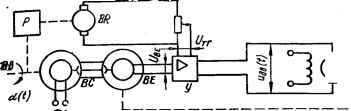 пв\ Рис. 6.3. Упрощенная принципиальная схема комбинированной следящей системы, связь по задающему воздействию в которой выполнена с помощью тахогенератора BR. новившаяся скоростная ошибка 6ауст (.). Эта ошибка, как известно, пропорциональна скорости alt т. е. 6ауСт (0 = Л; Dx — \lkp. В этом случае напряжение ошибки на выходе сельсина-приемника BE иве (О — стбкуст (-) = (kcJkp) ос-, а напряжение, поступающее на двигагель М, ыдв (.) = ива (t) = kyuBe (t) = fee«i = kCTkylkp, kCr, ky — коэффициенты прербразования сельсинов в трансформаторном режиме и усиления усилителя У соответственно), т. е. идв (t) пропорционально с*!- Таким образом, для вращения приемного вала со скоростью, равной скорости ctj вращения ведущего вала, на двигатель должно подаваться напряжение ыдв (0, пропорциональное этой скорости. В рассматриваемой системе с принципом управления по отклонению напряжение ыдв (.) целиком формируется из напряжения ошибки ые« {t), т. е. необходимая скорость вращения двигателя достигается только за счет ошибки. В комбинированной следящей системе (рис. 6.3), в которой связь по задающему воздействию реализована с помощью тахогенератора BR, с напряжением ошибки в усилителе у складывается напряжение тахогенератора: итг (t) — x0da (t)/dt — х. Как видим, напряжение «тг (0. как и напряжение ошибки «ве U), пропорционально скорости (частоте) вращения ах ВВ. Напряжение итг (t) усиливается и вместе с напряжением ошибки подается на двигатель: Ыдв (.) = «вес (0 + &у"тг (0. т. е. необходимое напряжение на входе двигателя ыдв (.) = &еа формируется из напряжения ошибки ыек (0 и напряжения тахогенератора kyUrr (t)- Благодаря этому при введении связи по задающему воздействию напряжение ошибки ыва (t) уменьшается. Перемещая Движок потенциометра R, можно изменять х0 и увеличивать составляющую напряжения куитг (.) на входе двигателя. В частности, если обеспечить выполнение условия kyx0 = k$, то ыдв (.) = fte«i = КуХ — = kyuTT (t), т. е. напряжение тахогенератора kyuT (t) полностью обеспечит вращение двигателя с требуемой скоростью. В этом случае ие< (0 — 0, а следовательно, и скоростная ошибка системы 6< уст (Q = 0. Устранение скоростной ошибки соответствует повышению астатизма системы с первого до второго порядка. Синтез связи по задающему воздействию из условия повышения порядка астатизма может быть выполнен с помощью изложенного в 118, 22] метода. С помощью связи по задающему воздействию возможно не только повышение динамической точности, но и улучшение переходных процессов САУ [18, 21, 22]. В следящих системах, в которых значительные ошибки вызываются как изменением задающего, так и возмущающим воздействием, вводят компенсационные связи по задающему и по возмущающему воздействиям. 6.5. Анализ качества комбинированных систем методом частотных характеристик Метод логарифмических частотных характеристик обычно используется для анализа и синтеза САУ с принципом управления по отклонению. Однако этот метод можно распространить и для расчета комбинированных систем автоматического управления [6, 18]. Как известно, при расчете САУ методом ЛЧХ оперируют логарифмической амплитудной частотной характеристикой (ЛАЧХ) разомкнутой системы по отклонению. С целью применения метода ЛЧХ для расчета и комбинированной следящей системы передаточную функцию (или передаточную функцию по ошибке) этой системы можно принять за передаточную функцию (или передаточную функцию по ошибке) эквивалентной по своим свойствам системы по отклонению и найти передаточную функцию эквивалентной системы по отклонению в разомкнутом состоянии. Затем исследование системы (анализ или синтез) можно проводить, используя эквивалентную ЛАЧХ, построенную на основании этой передаточной функции. Напомним, что передаточная функция /Се (р) по ошибке системы с принципом управления по отклонению и передаточная функция этой системы в разомкнутом состоянии Кр (р) связаны выражением Кв{р)=\/[1+Кр(Р)},(6.29) откуда Kp(p) = [i-Ke(P)]//Ce(p).(б.зо) Если имеется комбинированная следящая система и Квк (р) является ее передаточной функцией по ошибке, то, принимая Лек (р) за передаточную функцию по ошибке эквивалентной следящей системы с принципом управления по отклонению, определим передаточную функцию эквивалентной системы в разомкнутом состоянии Кэ.р (р) с помощью выражения, аналогичного выражению (6.30): Кэ.р (р) = [ 1 - Квк (р)]/Ке* (Р).(6.31) Для комбинированной системы (рис. 6.2) Квк (р) определяется выражением (6.27) Яек(/>) = П-К,(Р)/С„(А>)]/[1 +Кр(р)], *Р (/>)=»*! &>)*.(/»)• (6.32) Подставив данное значение Квк (р) в формулу (6.31), получим *э.р(р)= i,wk„w •(6-33) На основании полученного выражения для Кэ.р (р) строятся ЛЧХ эквивалентной системы по отклонению в разомкнутом состоянии. Используя метод вещественных частотных характеристик, строится кривая переходного процесса комбинированной системы и по ней определяются показатели качества. Пример 4. Определить Кэр (р) комбинированной следящей системы (рис. 6.2) имеющей Kt ip) = ki; К2 (р) = k„/(TlP + 1) (Г-р + 1) р; Кю (р) = ТоР. (6.34) Значения передаточных функций (6.34) подставляем в формулу (6.33) К (D\ = iM?> + 1) (TjP + О Р} (*ч + т„р) s-p v> 1 - WiTtf + 1) (Т2р + 1) p] т0р ~ h (1 + Гэр) вли где ?W + (Тг + Г2) + (i ki%o) p *э.р (P) = *э.р (1 + ТэРШа<жР* + «i„Pa + P) (6.35) t -bb - bkp ■ T - T° • a n -Л±Л. Если коэффициент тв найден из условия повышения порядка астатизма: 1 — kjtg = О, то формула (6.35) примет вид й- (1 + ГэР) р(1 + ГэР) Кэ.г,(Р) 9-pW (7>+l)p*. где Ае = kp/(Ti + ТУ — коэффициент усиления по ускорению эквивалентной системы в разомкнутом состоянии; Тэ1 = Ti-Vf7. + т2) — постоянная времени эквивалентной системы. Построив в соответствии с полученным выражением ЛЧХ эквивалентной системы, можно определить ее устойчивость, запасы устойчивости по фазе и амплитуде. Чтобы с помощью метода ВЧХ построить переходный процесс комбинированной системы, можно и не прибегать к определению Кэ.р (р) и построению ЛАЧХ. Представив комплексную передаточную функцию системы по ошибке в алгебраической форме Квк (ja>) = Рвк (®>) + + /QeK (й>), по выражению для Рек (») следует построить ВЧХ комбинированной системы для ошибки и по ней известным способом определить кривую переходной функции для ошибки Ле (-)• Переходная функция системы h (t) в случае необходимости находится по формуле h (t) = 1 he (tl 0 ... 61 62 63 64 65 66 67 ... 143 |












