Раздел: Документация
0 ... 66 67 68 69 70 71 72 ... 143 Пример вычисления среднеквадратической ошибки Вычислим СКО системы автоматического сопровождения цели радиолокационной станции (рис. 7.9). На вход системы поступает задающее воздействие (например, азимут цели) с наложенной помехой п (f). Входной сигнал системы <p (f) = a (f) + + п (t) сравнивается с управляемой величиной Р (г) (азимутом антенны) следящей системы. Разность 6С (г) = <р (г) — Р (г) поступает на усилитель следящей системы. Передаточная функция системы в разомкнутом состоянии Кр (Р) = [ftp (TiP + 1)]/[(7> + 1) Р\. Ошибка системы в (t) формулой (7.18) : А,&« -■ a (f) — р (f). Уравнение дли ошибки в 6 (Р) = Ква [р) а (р) + К3 (р) п (р). На основании формулы (7.7) запишем Se (со) = I Ква (/со) р Sa (со) + К3 (/со) р Sn (со), (7.26) соответствии с (7.27) где Ks(jo>) 1 (Га/со + 1) /со 1 + Л"р (/со) (Г2/со + 1) /со 4- fep (TJia + 1) = (Га/со+ 1)/со M/cop + U+VHco + fep ■ Кр (/со) kp (7\/со + 1) (7.28) (7.29) 1 + КР (/со) Т2 (/со)2 + (1 + *рГ,) /со + Ар Определим спектральную плотность полезного сигнала а (г) и помехи п (г). Предположим, что угловая координата цели а (/) относительно радиолокатора изменяется по графику, изображенному на рис. 7.10, а. Угловая скорость движения цели в течение некоторого интервала времени остается постоянной (рис. 7.10, б), причем моменты скачков и значения скоростей — случайные величины. Такие изменения скорости могут соответствовать маневрам цели. Из рисунка видно, что кривая a (t) не является стационарным случайным процессом. Поэтому с помощью рассматриваемого статистического метода, справедливого лишь для случая стационарных случайных процессов, нельзя найти преобразования сигнала a (f) системой. Однако в данном случае задача упрощается: поскольку a (г) поступает на вход астатической системы с астатизмом первого порядка, то ошибка по положению от а (/) равна нулю, Основная ошибка системы вызывается первой производной задающего воздействия, т. е. скоростью цели, поэтому нас будут интересовать статистические характеристики производной da (1)ldt. Первую производную от a (t) (рис. 7.10, б) можно считать стационарным случайным процессом. Если предположить, что продолжительность промежутков т[ подчиняется распределению Пуассона, то, как показано в [12], спектральная плотность производной da, (t)ldt Sa(co) = 2prf7(co2+P2),(7.30) где я2 — среднее значение квадрата скорости; 1/Р — средняя длина промежутков времени, в течение которых скорость остается постоянной. Если задающим воздействием считать da (f)ldt, а не а (г) (или в изображенное по Лапласу ра, (р), а не а (р)), то для получения передаточной функции системы в этом случае надо обе части выражения для передаточной функции Кца (р) = ЭС V(t)=<t(t)+n(i) e(t) Т,р*1 т. Рис. 7.9. Упрощенная структурная схема системы радиолокационной станции. автосопровождения цели Рис- 7.10. Графики изменения угловой координаты (а) и скорости (б) цели. = 6а (р)/а (р) разделить на р: KWPaWPiPh (7.31) В качестве помехи возьмем белый шум. имеющий спектральную плотность Sn (со) = с2 = const.(7.32) Подставив в выражение (7.27) значения Ква (/сй)//сои/С3 (/ш) из выражений (7.28) и (7.29) (при учете формулы (7.31)) и значения Sa (со) и Sn (со) из выражений (7.30) и (7.32), получим 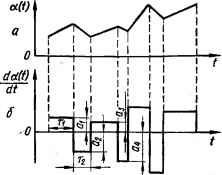 Se (со) Та/ю + 1 26а2 + Г2(/со)2 + (1 4-W/co + p Г2(/т)* + (1 +рГг)/со + р i6kh в соответст ющих: со* + р2 г с2, т. е. среднее значение квадрата ошибки в соответствии с формулой (7.19) можно представить в виде суммы двух составляющих: (7.33) где оо 7усо+1 1 " 2л J I Т. Г, (/со)2 + (1 + kpTj /со + fep со* + р2 kp (7усо + 1) 2(/co)2 + (l+*p71)/cu+fep dbi. (7.34) (7.35) Найдем сначала значение б2. Для этого приведем интеграл (7.34) к виду таблич- ного интеграла (7.24): вычислим квадрат модуля числителя Т2/и+12=7со2+1 и введем сомножитель (со2 -f- Р2) в знаменателе под знак модуля w2 + 62 = /co + 62. (7.36) (7.37) Учитывая формулы (7.36) и (7.37), запишем интеграл (7.34) в форме табличного интеграла 1 7 (7co2+l)rfco = % = 2Р°2 "2я" J I [Г, (/со)2 + (1+ крТг) /со + Ар] (/со + р) I2 (7fco2-f l)dco I Т2 (/со)3 + (1 + kpTx + рГ2) (/со)* + фкРТх + р + kp) /со + р*р 2 = 2ро»/3. (7.38) 209 Из сравнения интеграла (7.38) с табличным интегралом (7.24) следует: Н (/to) = Г2 (/со)з + (1 + kpTt + рГ8) (/to)8 + (рад + р + Ар) /to + рАр; G(cu) = 7cu2-f 1,} п = 3 — степень Н (/to) знаменателя подынтегрального выражения; а0=Т2; о1 = 1+АрГ1 + Р7,я; а2 = РА, + р + Ар; о3 = рАр; Значение табличного интеграла /3 согласно формулам (7.25) 1 o2fc„ + o06i — uffllas Ъх — аз/Дз 3 2а0 (охо2 — а0о3)2(0,02—0003) * Подставив в эту формулу значения коэффициентов из (7.39) и умножив /8 в соответствии с выражением (7.38) иа 2Ра2, получим 52 №4T22-(WPfi)(l + kpTt + fiT2)] В« (1 + АрГх + pr2) (pAprt + р + Ар) - Г2Арр *• Определим значение 6. Для приведения интеграла (7.35) к виду табличного интеграла (7.24) вычислим квадрат модуля числителя Г1/ш+Н2 = 7>»-т-1.(7.41) С учетом формулы (7.41) записываем интеграл (7.35) в форме табличного интеграла -2 1 Р(АрГсо2 + /ф da 2 en = c2T J Т2 (/со)2 + (1 + Ap7\j /to + Ар Р = **(7-42) Из сравнении интеграла (7.42) с табличным (7.24) имеем: Н (/со) = Т2 (/со)2 + (1 + ApTf) /со + Ар; G(co) = Ap7,2co2+Ар; п = 2, ао = Т2; аг = 1 + АрТ; а2 = Ар; fco = к1тЬ b\ = Ар. (7.43) (7.44) V i 1 — р- Значение табличного интеграла 12 в соответствии с формулой (7.25) 12 = (Ьв + + а0Ьх1а1аоа1- Подставив в эту формулу значения коэффициентов из формулы (7.44) и умножив /2 в соответствии с выражением (7.42) на с2, получим А„с2 (Г?А„ + Т2) (7"45) 7.3. Статистический метод синтеза оптимальных параметров САУ Задача статистического синтеза оптимальной системы Одной из важнейших задач теории автоматического управления является задача отыскания (синтеза) оптимальной системы. Оптимальной системой является система, наилучшая в каком-либо отношении. Определение оптимальной системы возможно лишь тогда, когда вы- 0 ... 66 67 68 69 70 71 72 ... 143 |












