Раздел: Документация
0 ... 67 68 69 70 71 72 73 ... 143 бран критерий оптимальности. Экстремальное значение этого критерия (минимум или максимум) определяет оптимальную систему. При поступлении на вход САУ задающего воздействия a (f) и помехи п (t), являющихся случайными функциями, правильный выбор системы может быть основан на статистическом критерии оптимальности. Наиболее широкое применение получил метод синтеза оптимальных систем на основе критерия минимума среднеквадратической ошибки, как сравнительно простой. Постановка задачи синтеза состоит в следующем. Пусть на вход системы (см. рис. 7.5) поступают задающее воздействие a (f) и помеха п (/), представляющие стационарные случайные процессы с известными спектральными плотностями и нулевыми средними значениями. Необходимо преобразовать полезный сигнал а (/) на входе в сигнал h (t) на выходе в соответствии с формулой h(p) = Н (р) а (р), где Н (р) — заданная преобразующая передаточная функция. Задача синтеза состоит в определении физически реализуемой передаточной функции системы Кз (р) или импульсной переходной функции k (t), при которой обеспечивается минимум среднего значения квадрата ошибки т 6* = ton-1- j \h(t) — $(t)}zdt между требуемым значением выходной величины h(f) и реальны ана- чением выходной величины В (/). Статистический метод синтеза оптимальных параметров системы Поставленная выше задача является общей задачей синтеза оптимальной системы. Рассмотрим частную задачу синтеза — задачу определения оптимальных параметров системы, имеющую также большое практическое значение. Постановка частной задачи синтеза состоит в следующем. Структурная схема системы задана. Требуется определить оптимальные значения некоторых параметров уже выбранной схемы системы, при которых среднее значение квадрата ошибки принимает минимальное значение (в2 = min). Решение этой задачи приведем на примере следящей системы. При поступлении на вход системы (см. рис. 7.5) задающего воздействия а (/) и помехи п (t) средний квадрат ошибки системы в соответствии с формулой (7.19) б2 = ё! + ё!(7.46) • где el -i- j tfea(/co)2S«(co)dor, —оо со (7.47) 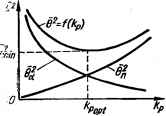 Из формулы (7.76) видно, что ошибка системы состоит из двух составляющих. Одна из них 9а (f) вызывается задающим воздействием (система не может точно воспроизводить задающее воздействие даже при отсутствии помехи). Другая составляющая 9П (/) возникает в результате частичного воспроизведения системой помехи. Обычно при стрем-*Рис. 7.11. Графическое опреде- лении уменьшить первую составляющую леиие кропт.(например, за счет повышения коэффи- циента усиления системы) увеличивается вторая составляющая ошибки (при повышении коэффициента усиления расширяется полоса пропускания системы, улучшаются условия про-. хождения высокочастотной помехи на выход системы) и наоборот. Таким образом, задача синтеза состоит в том, чтобы выбрать оптимальные параметры системы; при которых суммарная ошибка является минимально возможной. Пусть требуется определить оптимальные значения двух параметров, например коэффициента усиления системы в разомкнутом состоянии kp и постоянной времени 7\ корректирующего устройства (см. формулу (7.26)). Предварительно интегралы (7.34) и (7.35) приводятся к виду табличных интегралов (7.24) и вычисляются значения 9« и 9 (см., например, формулы (7.40) и (7.45)). Как видно из формул, 9«, 9п и 6а являются функциями искомых параметров kp и 7\ i Wa = ft (kp, Ti); 9n = f2 (kp, 7\); 9a = /3 (kp, 7\). Для определения оптимальных значений kp и 7\, соответствующих минимуму б2, вычисляют частные производные по kp и 7\ и приравнивают их нулю: d&ldkp = 0; d№ldTt = 0, в результате получают два уравнения с двумя неизвестными, из которых определяют искомые оптимальные значения kp опт и Т{ опт. Чтобы убедиться в том, что получен минимум 9а, а не максимум, вычисляют G2 при полученных значениях kponT нТ1оП11и при значениях, близких к ним. Дисперсия ошибки G2 при других значениях kp и Т{ должна оказаться больше. Оптимальные значения параметров также можно определить графически. Задаваясь рядом значений параметра (например, kp), вычисляют по формулам (7.40) и (7.45) значения 9„ и 9п. Для наглядности строятся графики зависимости 9„ = fx (kp) и 9fi = /2 (kp) (рис. 7.11). Суммируя ординаты этих графиков, строят график зави. симости 92 = /д (kp), из которого определяют оптимальное значение бропт, соответствующее 6min. График зависимости 92 = f3 (kp) можно построить и не прибегая к построению отдельных графиков 6 = = h (&Р) и 9 = /2 (kp). Аналогично определяются оптимальные значения и других яараметров. Как уже отмечалось, если параметры системы выбраны из условия получения минимума СКО, то замкнутая система обычно имеет слабо-ватухающий переходный процесс. Поэтому после расчета оптимальных параметров необходимо определить показатели качества переходного процесса. Рациональное решение находится как компромиссное. Кроме того, при найденных оптимальных параметрах необходимо проверить, чтобы статические свойства системы также отвечали требованиям (коэффициент усиления kp был не меньше необходимого с точки зрения статики). Пример 2. На вход следящей системы (рис. 7.12) поступают задающее воздействие а (/) и помеха л (/), спектральные плотности которых соответственно Sa (to) = = а22с/(с2 + to2); Sn (to) = а*. Определить оптимальное значение коэффициента усиления kp системы, при котором в2 = min. В соответствии с формулой (7.19) дисперсия ошибки системы 00ОС ®2 == ~Ш 1 (/«>) I2 Sa И dw + "5Г j I Ks №>) I2 Sn («) dco = 6 + ё£. —ос—oo(7.48) Определяем передаточные функции „1 /toKp (A*)h *е« </">>- 1+кр(/ш) - /со-f kp : *iO«>>- l + Kp(/to) /03 + kp и их значения подставляем в формулу (7.48). Дисперсия составляющей ошибки, вызываемой а (/), В2 = J— С I2 °22с л „20 1 Гc02dc0 °« 2я J /со+А„ с2 + со2 Ш °" 2л J (/со + Ар)(с + /со) I2 —ОО -ОО Из сравнения интеграла (7.49) с табличным интегралом (7.24) следует: Н (/со) = (/со)2 + (Ар + с) /со + kpc; G(co) = co2; и = 2; 00=1; ах = Ар + с; Оз = fepc; Ь0=1; fcj = 0. Находим табличный интеграл , fep + врУдг 1 22000!2(Ар + с) и подставим его значение в формулу (7.49): § = а2с/(Ар + с).(7.50) Дисперсия составляющей ошибки, вызываемой помехой п (f): -ОО-ОО Из сравнения интеграла (7.51) с табличным интегралом (7.24) следует: Н (/со) = /со + kp\ G (ю) = 1; л=1; о0 = 1; а, = АР; 60= 0 ... 67 68 69 70 71 72 73 ... 143 |












