Раздел: Документация

0 ... 76 77 78 79 80 81 82 ... 143

—. с		f(f> = f In. е]	— ■с- II к Sir	IIS ь. II	/=>(?, e) = D {/[". е]} v{f(d)	F (г, e) = Z{fr«)} = = Z {Fr(P)}
1.	Единичный скачок 1 (t)	1 (Ъ = 1 [п]	I р	1 я	е« е« —1	г г—1
2.	Линейно-возрастающая функция t	7= п+ е	1 ~¥	1	е" е« ---]--е (e»—I)2 е* — 1	Гг Тг --1--е (г—I)2 1 г—1
3.	Квадратичная функция г2	I2 = (п + е)2	2! V	2!	е*(е+1) (е» — I)3 е« + 2-е + (е9— I)2 е«—I	2 Гг + (г-If т (1+2е)Г2г + (г-1)2 (Ге)*г f г—1
4.	Экспонента e±ai	е±а7 е±а (п+е)	1	1	е" с±ае
				Я + а	е9-е±а	г-е±аТ
5.	Скачок и экспонента 1-е±0	1 е±а «= 1 е±а (п+е)	а	а	е* е,9	г
			Р (р Т а)		е? 1 е?-е±а	г— 1 ±07" г — е

---

а) Непрерывный модулирующий сигнал

А

№

tI00

6) Немодулированная последовательность импульсов ■ Амплитудный • спектр ifnTJ

2Т4Т

пТ

-2ис -0)0 О Шо 2о)0

О)

в) Модулированная последовательность импульсов одш.

fbTh

Смодулированная решетчатая функция

пТГГГГгг

пТ

rl\/i

-20о -Шо.РПЫяо 2tiB

а)

Дополнительные Основная Дополнительные Составляющие спектра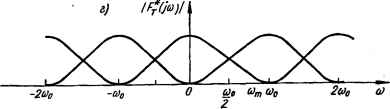

Рис. 8.26. Изменения сигналов во времени и их амплитудно-частотные спектры:

а, б, в ■

<s>m < Юо/2; г — o>m > aj2.

сов i [пТ], разложив в ряд Фурье, можно представить в виде суммь постоянной составляющей (со = 0), первой гармоники с частотой со0 = = 2п1Т и бесконечного количества гармоник, отличающихся друг от Друга по частоте на со0, с амплитудой ИТ (рис. 8.26, б). Изображение Фурье амплитудно-модулированной последовательности импульсов / [пТ] определяется выражением

/=г(/со)=(1/Г) £ (/со —/псоо),

(8.31)

1 239

---

т. е. частотный спектр решетчатой функции получается суммированием частотных спектров, соответствующих непрерывной функции, смещенных по оси частот на величины исо0, где п изменяется от —оо до +оо (рис. 8.26, в). Таким образом, действие простейшего импульсного элемента сказывается в появлении боковых полос частот, идентичных спектру непрерывной функции.

Формула связи (8.31) позволяет по преобразованию Фурье FT (/со) непрерывной функции /т (t) определить дискретное преобразование Фурье FT (/с°) решетчатой функции / [пТ]. Формула (8.31) справедлива в случае нулевого начального значения функции / [0] = 0. В общем случае, когда / [0] Ф 0, формула связи имеет вид

оо

Ff(/co) = /[0]/2 + (l/r) £ (/со — /rtco0).

Л——оо

Преобразование Лапласа решетчатой функции определяется выражением, аналогичным последнему выражению

оо

Ff(p)=/[0]/2 + (ЦТ) £ FT(p — jtm0).(8.32)

П -—оо

Операцию рассмотренного преобразования обозначают ® \FT (р)} FT(p)=®{FT(p)}=-Lf[0)+Jr V FT(p-im)o). (8.33)

Z1 П=—оо

Это преобразование называют прямым -преобразованием.

При использовании относительного масштаба времени формула связи (8.32) примет вид

Р*(Я) =4"£ F(q + 2njn), q=PT,

П=—оо

а для смещенной решетчатой функции

оо

F* (q, е)= £ &Vtof**F (q + 2njn). (8.34)

П=—оо

Таким образом, дискретное преобразование можно найти по формуле

оо

F*(q, е) = D [f\n. в]} - £ / [п. 8] в"*", если известна решетчатая функция / [п, е], или по формуле

со

F* (q, е) = ф F (q)} = V е«+2л,шр ц + 2щП),

П——оо

если известно непрерывное преобразование Лапласа F (q).

Для определения дискретного преобразования Лапласа F* (q, в) (например, для определения дискретной передаточной функции системы /(р (q, в)) по обычному изображению Лапласа F (q) (по передаточ-

0 ... 76 77 78 79 80 81 82 ... 143